题目内容
如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上．（1）求证：△APN∽△ABC；
（2）若这个矩形的长是宽的2倍，则宽是多少mm？
考点：相似三角形的应用
专题：
分析：（1）根据矩形的对边平行得到BC∥PN，利用“平行于三角形的一边的直线截其他两边或其他两边的延长线，得到的三角形与原三角形相似”判定即可．
（2）设宽为xmm，则长为2xmm，同（1）列出比例关系求解，但是要注意有两种情况，PQ可以为长也可以为宽，分两种情况分别求解即可．
（2）设宽为xmm，则长为2xmm，同（1）列出比例关系求解，但是要注意有两种情况，PQ可以为长也可以为宽，分两种情况分别求解即可．
解答：解：（1）∵四边形PNQM为矩形，
∴BC∥PN，
∴△APN∽△ABC；
（2）设边宽为xmm，则长为2xmm，
∵四边形PNMQ为矩形，
∴PN∥BC，PQ∥AD，
根据平行线的性质可以得出：
=
、
=
，
①PQ为长，PN为宽：
由题意知PQ=2xmm，AD=80mm，BC=120mm，AP=xmm，
即
=
，
=
，
∵AP+BP=AB，
∴
+
=1，
解得x=30，2x=60．
即长为60mm，宽为30mm．
②PQ为宽，PN为长：
由题意知PQ=xmm，AD=80mm，BC=120mm，AP=2xmm，
即
=
，
=
，
∵AP+BP=AB，
∴
+
=1，
解得x=
，2x=
．
即长为
mm，宽为
mm．
答：矩形的长为60mm，宽是30mm或者长为
mm，宽为
mm．
∴BC∥PN，
∴△APN∽△ABC；
（2）设边宽为xmm，则长为2xmm，
∵四边形PNMQ为矩形，
∴PN∥BC，PQ∥AD，
根据平行线的性质可以得出：
| PQ |
| AD |
| BP |
| AB |
| PN |
| BC |
| AP |
| AB |
①PQ为长，PN为宽：
由题意知PQ=2xmm，AD=80mm，BC=120mm，AP=xmm，
即
| 2x |
| 80 |
| BP |
| AB |
| x |
| 120 |
| AP |
| AB |
∵AP+BP=AB，
∴
| 2x |
| 80 |
| x |
| 120 |
解得x=30，2x=60．
即长为60mm，宽为30mm．
②PQ为宽，PN为长：
由题意知PQ=xmm，AD=80mm，BC=120mm，AP=2xmm，
即
| x |
| 80 |
| BP |
| AB |
| 2x |
| 120 |
| AP |
| AB |
∵AP+BP=AB，
∴
| x |
| 80 |
| 2x |
| 120 |
解得x=
| 240 |
| 7 |
| 480 |
| 7 |
即长为
| 480 |
| 7 |
| 240 |
| 7 |
答：矩形的长为60mm，宽是30mm或者长为
| 480 |
| 7 |
| 240 |
| 7 |
点评：本题考查了正方形以及矩形的性质，结合了平行线的比例关系求解，注意数形结合的运用．
练习册系列答案
阅读快车系列答案
相关题目
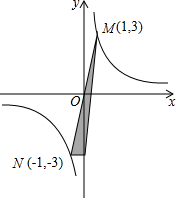如图，求阴影部分的面积．
在Rt△ABC中，AC=BC=8，∠C=90°，点D为BC中点，将△ABC绕点D逆时针旋转45°，得△A′B′C′，B′C′与AB交于点E，则S△CDE=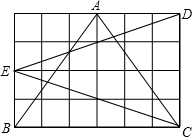
如图是单位长度为1的网格，比较图中△ABC和△CDE的面积、周长的大小．