题目内容
4.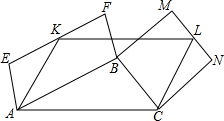 在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.
在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.
分析 首先过点B作GH⊥AK于点G,交CL于点H,连接BK,BL,可得S△ABK+S△BCL=$\frac{1}{2}$S?AKLC,S△ABK=$\frac{1}{2}$S?AEFB,S△BCL=$\frac{1}{2}$S?BCNM,即可证得结论.
解答 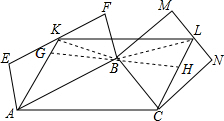 解:S?AKLC=S?AEFB+S?BMNC.
解:S?AKLC=S?AEFB+S?BMNC.
理由:过点B作GH⊥AK于点G,交CL于点H,连接BK,BL,
∵四边形AKLC是平行四边形,
∴AK∥CL,AK=CL,
∴GH⊥CL,
∴S△ABK+S△BCL=$\frac{1}{2}$AK•BG+$\frac{1}{2}$CL•BH=$\frac{1}{2}$AK•(BG+BH)=$\frac{1}{2}$AK•GH=$\frac{1}{2}$S?AKLC,
∵S△ABK=$\frac{1}{2}$S?AEFB,S△BCL=$\frac{1}{2}$S?BCNM,
∴S?AKLC=S?AEFB+S?BMNC.
点评 此题考查了平行四边形的性质以及三角形面积问题.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
9.已知抛物线y=ax2+2ax+m(a>0)经过点(-4,y1)、(-2,y2),(1,y3),则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y2>y1 | C. | y1>y3>y2 | D. | y3>y1>y2 |
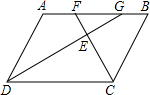 如图,平行四边形ABCD中,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G.AD=6,DC=8,求证:AF=BG.
如图,平行四边形ABCD中,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G.AD=6,DC=8,求证:AF=BG.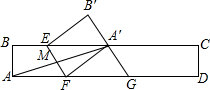 如图,在矩形ABCD中,AB=1,AD=6,F是AD上的点,且AF=2,E在BC上,沿EF折叠,使点A落在BC边上的点A′处,G是FD上的动点,连接AA′、A′G,当△AA′G为直角三角形时,AG的值为4或2+$\sqrt{3}$.
如图,在矩形ABCD中,AB=1,AD=6,F是AD上的点,且AF=2,E在BC上,沿EF折叠,使点A落在BC边上的点A′处,G是FD上的动点,连接AA′、A′G,当△AA′G为直角三角形时,AG的值为4或2+$\sqrt{3}$.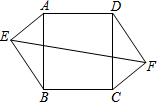 如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD外的两点,且AE=FC=3,BE=DF=4,则EF的长为7$\sqrt{2}$.
如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD外的两点,且AE=FC=3,BE=DF=4,则EF的长为7$\sqrt{2}$. 如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.
如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.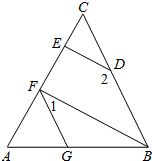 如图,∠AGF=∠ABC,∠1+∠2=180°,
如图,∠AGF=∠ABC,∠1+∠2=180°,