题目内容
19.计算.(1)$\sqrt{2}$($\sqrt{2}$-$\sqrt{3}$)+$\sqrt{6}$;
(2)$\sqrt{2}$×(-$\sqrt{32}$-2$\sqrt{18}$+3$\sqrt{10}$);
(3)($\sqrt{2}$-$\sqrt{3}$)2+($\sqrt{3}$+$\sqrt{2}$)2015•($\sqrt{3}$-$\sqrt{2}$)2016.
分析 (1)直接利用二次根式乘法运算法则得出答案;
(2)首先化简二次根式,进而利用二次根式乘法运算法则得出答案;
(3)利用乘法公式结合积的乘方运算法则得出答案.
解答 解:(1)$\sqrt{2}$($\sqrt{2}$-$\sqrt{3}$)+$\sqrt{6}$
=2-$\sqrt{6}$+$\sqrt{6}$
=2;
(2)$\sqrt{2}$×(-$\sqrt{32}$-2$\sqrt{18}$+3$\sqrt{10}$)
=$\sqrt{2}$×(-4$\sqrt{2}$-6$\sqrt{2}$+3$\sqrt{10}$)
=-20+6$\sqrt{5}$;
(3)($\sqrt{2}$-$\sqrt{3}$)2+($\sqrt{3}$+$\sqrt{2}$)2015•($\sqrt{3}$-$\sqrt{2}$)2016
=2+3-2$\sqrt{6}$+[($\sqrt{3}$+$\sqrt{2}$)×($\sqrt{3}$-$\sqrt{2}$)]2015×($\sqrt{3}$-$\sqrt{2}$)
=5-2$\sqrt{6}$+$\sqrt{3}$-$\sqrt{2}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
4.把x3+x2y-xy2-y3分解因式,标准答案是( )
| A. | (x+y)(x2-y2) | B. | x2(x+y)-y2(x+y) | C. | (x+y)(x-y)2 | D. | (x+y)2(x-y) |
5.下列说法正确的是( )
| A. | 两个有理数的积一定大于任何一个因数 | |
| B. | 两个互为倒数的积为正数 | |
| C. | 一个数和它的相反数的积一定是0 | |
| D. | 任何一个数都大于它的倒数 |
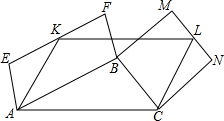 在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.
在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由. 如图,正方形ABCD的面积为36cm2,点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画$\widehat{AC}$,连接AF,CF,则图中阴影部分的面积为9πcm2.
如图,正方形ABCD的面积为36cm2,点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画$\widehat{AC}$,连接AF,CF,则图中阴影部分的面积为9πcm2.