题目内容
14.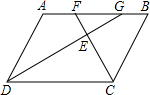 如图,平行四边形ABCD中,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G.AD=6,DC=8,求证:AF=BG.
如图,平行四边形ABCD中,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G.AD=6,DC=8,求证:AF=BG.
分析 由平行四边形ABCD中,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G,易证得△ADG与△BCF是等腰三角形,继而证得结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,
∴∠AGD=∠CDG,∠BFC=∠DCF,
∵∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G,
∴∠ADG=∠CDG,∠BCF=∠DCF,
∴∠ADG=∠AGD,∠BFC=∠BCF,
∴AG=AD,BC=BF,
∴AG=BF,
∴AF=BG.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△ADG与△BCF是等腰三角形是解此题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.下列各式中正确的是( )
| A. | (a-b)2=a2-b2 | B. | (a+2b)2=a2+2ab+b2 | C. | (a+b)2=a2+b2 | D. | (-a+b)2=a2-2ab+b2 |
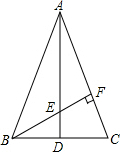 如图,在△ABC中,AB=AC,点D是BC的中点,BF⊥AC于点F,交AD于点E,∠BAC=45°.求证:△AEF≌△BCF.
如图,在△ABC中,AB=AC,点D是BC的中点,BF⊥AC于点F,交AD于点E,∠BAC=45°.求证:△AEF≌△BCF.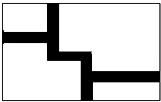 如图,在长为32 米,宽为20 米的矩形地面上修建同样宽度的道路(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽是多少米?
如图,在长为32 米,宽为20 米的矩形地面上修建同样宽度的道路(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽是多少米?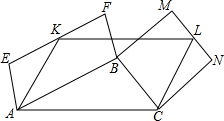 在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.
在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.