题目内容
10.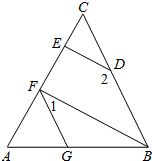 如图,∠AGF=∠ABC,∠1+∠2=180°,
如图,∠AGF=∠ABC,∠1+∠2=180°,(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
分析 (1)根据∠AGF=∠ABC可得出BC∥GF,进而可得出∠AFG=∠C,再根据角的计算可得出∠1=∠CDE,由此即可得出∠CED=∠CFB,根据“同位角相等,两直线平行”即可得出BF∥DE;
(2)根据DE⊥AC、BF∥DE即可得出∠AFB=90°,再结合∠1+∠2=180°、∠2=150°以及∠AFB=∠AFG+∠1即可算出∠AFG的度数.
解答 (1)证明:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠AFG=∠C.
∵∠1+∠2=180°,∠CDE+∠2=180°,
∴∠1=∠CDE.
∵∠CED=180°-∠C-∠CDE,∠CFB=180°-∠AFD-∠1,
∴∠CED=∠CFB,
∴BF∥DE.
(2)解:∵DE⊥AC,BF∥DE,
∴∠AFB=∠AED=90°,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°.
∵∠AFB=∠AFG+∠1=90°,
∴∠AFG=60°.
点评 本题考查了平行线的判定与性质,解题的关键是:(1)找出∠CED=∠CFB;(2)找出∠1=30°.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
相关题目
1.解方程$\frac{4}{3}$(x-1)-1=$\frac{1}{3}$(x-1)+4的最佳方法是( )
| A. | 去括号 | B. | 去分母 | C. | 移项合并(x-1)项 | D. | 以上方法都可以 |
5.下列说法正确的是( )
| A. | 两个有理数的积一定大于任何一个因数 | |
| B. | 两个互为倒数的积为正数 | |
| C. | 一个数和它的相反数的积一定是0 | |
| D. | 任何一个数都大于它的倒数 |
15.下面各式中,$\frac{1}{3}$x+$\frac{1}{2}$y,$\frac{1}{xy}$,$\frac{1}{5+a}$,-4xy,$\frac{x}{π}$,分式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.方程(m-2)x2+3mx+1=0是关于x的一元二次方程,则( )
| A. | m≠±2 | B. | m=2 | C. | m=-2 | D. | m≠2 |
19.点P在正方形ABCD内,且△PAB是等边三角形,那么∠DCP为( )
| A. | 15° | B. | 18° | C. | 22.5° | D. | 30° |
20.已知点(-3,y1),(3,y2)都在直线y=$\frac{1}{5}$x+2上,则y1和y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
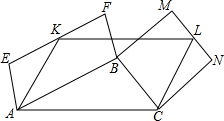 在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.
在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.