Question

9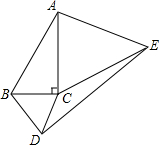．如图，分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE，∠ACB=90°，∠BAC=30°，BC=1，求DE的长．

Answer 1

分析 连接BE，首先由含30度角的直角三角形的性质和勾股定理求出AB和AC的长，再判定△ABE是直角三角形，由勾股定理得到BE的长，由SAS证得△BCE≌△DCE，即可得出结果．

解答 解：连接BE，如图所示：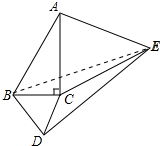
∵在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=1，
∴AB=2BC=2，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∵△ACE为等边三角形，
∴∠CAE=∠ACE=60°，AC=AE=$\sqrt{3}$，
∴∠BAE=∠BAC+∠CAE=30°+60°=90°，∠BCE=90°+60°=150°，
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{2}^{2}+（\sqrt{3}）^{2}}$=$\sqrt{7}$，
∵△BCD是等边三角形，
∴BC=CD，∠BCD=60°，
∴∠DCE=360°-150°-60°=150°=∠BCE，
在△BCE和△DCE中，
$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCE=∠DCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$，
∴△BCE≌△DCE（SAS），
∴DE=BE=$\sqrt{7}$．

点评 本题考查了勾股定理、等边三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．