题目内容
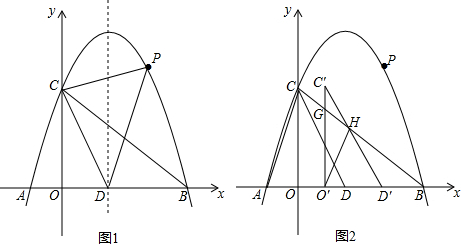
12. 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OP=3,PD=1,则OC=3$\sqrt{2}$.
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OP=3,PD=1,则OC=3$\sqrt{2}$.
分析 根据AO⊥OC,CD⊥OD,得到∠AOC=∠D=90°,求得∠DPC=∠OAC,于是得到∠ACO=∠ACD,证得AC平分∠OCD,根据角平分线定理得到$\frac{OC}{CD}=\frac{OP}{PD}$=3:1,设OC=3k,CD=k,根据勾股定理即可得到结论.
解答 解:∵AO⊥OC,CD⊥OD,
∴∠AOC=∠D=90°,
∴∠OAP+∠ACO=∠DPC+∠DCP=90°,
∵OA=OP,
∴∠OAP=∠APO,∵∠APO=∠DPC,
∴∠DPC=∠OAC,
∴∠ACO=∠ACD,
∴AC平分∠OCD,
∴$\frac{OC}{CD}=\frac{OP}{PD}$=3:1,
设OC=3k,CD=k,
∵OD2+CD2=OC2,
即42+k2=(3k)2,
∴k=$\sqrt{2}$,
∴OC=$3\sqrt{2}$,
故答案为:3$\sqrt{2}$.
点评 本题考查了角平分线定理,垂直的定义,勾股定理,等腰三角形的性质,熟练掌握角平分线定理是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目

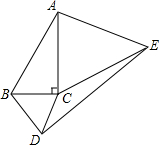 如图,分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE,∠ACB=90°,∠BAC=30°,BC=1,求DE的长.
如图,分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE,∠ACB=90°,∠BAC=30°,BC=1,求DE的长. 如图所示,直线AC∥m∥OB,AP,OP分别是∠CAO与∠AOB的平分线,直线m经过点P,AC与直线m的距离和OB与直线m的距离相等吗?请说明理由.
如图所示,直线AC∥m∥OB,AP,OP分别是∠CAO与∠AOB的平分线,直线m经过点P,AC与直线m的距离和OB与直线m的距离相等吗?请说明理由.

 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$,以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则$\frac{PF}{PE}$=$\frac{12}{25}$.
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$,以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则$\frac{PF}{PE}$=$\frac{12}{25}$.