题目内容
4. 如图,以只蚂蚁沿着长AB=7,宽BC=5,高CD=5的长方体木箱表面的A点爬到D点,则它爬过的最短路程为$\sqrt{149}$.
如图,以只蚂蚁沿着长AB=7,宽BC=5,高CD=5的长方体木箱表面的A点爬到D点,则它爬过的最短路程为$\sqrt{149}$.
分析 将长方体展开,可分三种情况,求出其值最小者,即为最短路程.
解答 解:展开图有3种情形如图,
在图1中AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
在图2中AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{{7}^{2}+1{0}^{2}}$=$\sqrt{149}$,
在图3中AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∵$\sqrt{149}$<13,
∴蚂蚁爬过的最短路程为$\sqrt{149}$.
故答案为$\sqrt{149}$.
点评 此题依据“两点之间,线段最短”,考查了长方体的侧面展开图,解答时利用勾股定理进行分类讨论是解题的关键.

练习册系列答案
相关题目
19.下列汽车标志中,是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x,y的值.
由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x,y的值.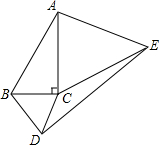 如图,分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE,∠ACB=90°,∠BAC=30°,BC=1,求DE的长.
如图,分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE,∠ACB=90°,∠BAC=30°,BC=1,求DE的长. 如图,C为BE上的点,CA⊥AB于点A,CD⊥BE于点C,AB=CE,AB∥DE,∠D=30°,求∠ACE的度数.
如图,C为BE上的点,CA⊥AB于点A,CD⊥BE于点C,AB=CE,AB∥DE,∠D=30°,求∠ACE的度数.