Question

1．如图，已知正方形ABDE和正方形AGFC中，点B、A、C在一条直线上，点G在边AE上，连接BG、EC．
（1）求证：BG=EC；
（2）观察图形，猜想BG与CE之间的位置关系，并证明你的猜想．

Answer 1

分析 （1）根据正方形的性质可得AB=AE，AC=AG，∠BAE=∠GAC=90°，然后利用“边角边”证明△ABG和△AEC全等，根据全等三角形对应边相等可得BG=EC；
（2）全等三角形对应角相等可得∠ABG=∠AEC，设BG的延长线交EC于H，然后求出∠ABG+∠ACE=90°，从而得到∠BHC=90°，再根据垂直的定义证明即可．

解答 证明：（1）在正方形ABDE和正方形AGFC中，AB=AE，AC=AG，∠BAE=∠GAC=90°，
在△ABG和△AEC中，
$\left\{\begin{array}{l}{AB=AE}\\{∠BAE=∠GAC=90°}\\{AC=AG}\end{array}\right.$，
∴△ABG≌△AEC（SAS），
∴BG=EC，
（2）∵△ABG≌△AEC，
∴∠ABG=∠AEC，
设BG交EC于H，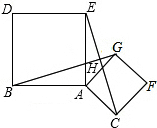

∵∠AEC+∠ACE=90°，
∴∠ABG+∠ACE=90°，
∴∠BHC=180°-90°=90°，
∴BG⊥EC．

点评 本题考查了正方形的性质，全等三角形的判定与性质，熟练掌握三角形全等的判定方法并根据正方形的性质找出全等的条件是解题的关键，此类题目，各小题的求解思路相同是解题的突破点．