题目内容
9.估计$\sqrt{27}$×$\sqrt{\frac{1}{3}}$$+\sqrt{20}$的运算结果应在( )| A. | 5到6之间 | B. | 6到7之间 | C. | 7到8之间 | D. | 8到9之间 |
分析 先利用二次根式的乘法法则计算得到原式=3+2$\sqrt{5}$,然后进行无理数的估算.
解答 解:原式=$\sqrt{27×\frac{1}{3}}$+2$\sqrt{5}$
=3+2$\sqrt{5}$,
∵$\sqrt{5}$≈2.236,
∴7<3+2$\sqrt{5}$<8.
故选C.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.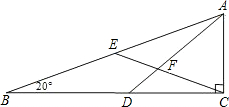 如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
 如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
18.已知a>0,则下列计算正确的是( )
| A. | $\sqrt{a}$+$\sqrt{a}$=$\sqrt{2a}$ | B. | $\sqrt{{a}^{2}}$-$\sqrt{a}$=$\sqrt{a}$ | C. | $\sqrt{a}×\sqrt{a}$=a2 | D. | $\sqrt{a}$$÷\sqrt{a}$=1 |
 如图,是小明学习三线八角时制作的模具,经测量∠2=100°,要使木条a与b平行,则∠1的度数必须是80°.
如图,是小明学习三线八角时制作的模具,经测量∠2=100°,要使木条a与b平行,则∠1的度数必须是80°. 几何证明.
几何证明. 如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.
如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P. 已知,如图,在四边形ABCD中,AB=CD,∠BAC=∠ACD,求证:△ABC≌△CDA.
已知,如图,在四边形ABCD中,AB=CD,∠BAC=∠ACD,求证:△ABC≌△CDA.