题目内容
4．
几何证明．如图，已知AB∥CD，BC交AB于B，BC交CD于C，∠ABE=∠DCF，求证：BE∥CF．
分析 根据平行线的性质得出∠ABC=∠DCB，求出∠EBC=∠FCB，根据平行线的判定推出即可．
解答 证明：∵AB∥CD，
∴∠ABC=∠DCB，
∵∠ABE=∠DCF，
∴∠ABC-∠ABE=∠DCB-∠DCF，
∴∠EBC=∠FCB，
∴BE∥CF．
点评 本题考查了平行线的性质和判定的应用，能求出∠EBC=∠FCB是解此题的关键，注意：内错角相等，两直线平行，反之亦然．
练习册系列答案
相关题目
15．下列分式是最简分式的（ ）
| A． | $\frac{a+b}{{{a^2}+{b^2}}}$ | B． | $\frac{a}{{{a^2}-3a}}$ | C． | $\frac{2a}{{3{a^2}b}}$ | D． | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |
12．
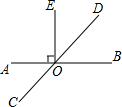如图，直线AB，CD相交于点O，OE⊥AB于O，若∠BOD=40°，则不正确的结论是（ ）
如图，直线AB，CD相交于点O，OE⊥AB于O，若∠BOD=40°，则不正确的结论是（ ）| A． | ∠AOC=40° | B． | ∠COE=130° | C． | ∠EOD=40° | D． | ∠BOE=90° |
观察数表，若用有序整数对（m，n）表示第m行第n列的数，如（4，3）表示实数6，则（20，18）表示的数是37．
9．估计$\sqrt{27}$×$\sqrt{\frac{1}{3}}$$+\sqrt{20}$的运算结果应在（ ）
| A． | 5到6之间 | B． | 6到7之间 | C． | 7到8之间 | D． | 8到9之间 |
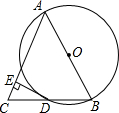如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC，垂足为E．
在2011元旦化妆晚会上，学生小明自制了一个无底圆锥形纸帽，如图所示，围成这个纸帽的面积是48πcm2．