题目内容
5.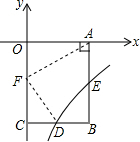 如图,已知B(4,-6),BA⊥x轴于点A,BC⊥y轴于点C,双曲线y=$\frac{k}{x}$(x>0)经过BC的中点D,且与AB交于点E.
如图,已知B(4,-6),BA⊥x轴于点A,BC⊥y轴于点C,双曲线y=$\frac{k}{x}$(x>0)经过BC的中点D,且与AB交于点E.(1)求反比例函数的解析式;
(2)若点F是OC上一点,且△FDC∽△AFO,求经过E,F两点的一次函数的解析式.
分析 (1)根据中点坐标公式得到点D的坐标,再根据待定系数法即可得到反比例函数的解析式;
(2)先把E的横坐标4代入反比例函数的解析式,得到E的坐标;再根据相似三角形的性质得到点F的坐标,再根据待定系数法即可得到经过E,F两点的一次函数的解析式.
解答 解:(1)∵B(4,-6),BC⊥y轴于点C,
∴点D的坐标为(2,-6),
∵双曲线y=$\frac{k}{x}$(x>0)经过BC的中点D,
∴-6=$\frac{k}{2}$,
解得k=-12.
故反比例函数的解析式为y=-$\frac{12}{x}$;
(2)当x=4时,y=-$\frac{12}{x}$=-$\frac{12}{4}$=-3,
则点E的坐标为(4,-3),
∵△FDC∽△AFO,
∴$\frac{FC}{AO}$=$\frac{CD}{OF}$,即$\frac{6-OF}{4}$=$\frac{2}{OF}$,
解得OF=2或OF=4,
∴点F的坐标为(0,-2)或(0,-4),
①当点F的坐标为(0,-2)时,设经过E,F两点的一次函数的解析式为y=k1x+b1,
则$\left\{\begin{array}{l}{{b}_{1}=-2}\\{4{k}_{1}+{b}_{1}=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-\frac{1}{4}}\\{{b}_{1}=-2}\end{array}\right.$.
故经过E,F两点的一次函数的解析式为y=-$\frac{1}{4}$x-2;
②当点F的坐标为(0,-4)时,设经过E,F两点的一次函数的解析式为y=k2x+b2,
则$\left\{\begin{array}{l}{{b}_{2}=-4}\\{4{k}_{2}+{b}_{2}=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=\frac{1}{4}}\\{{b}_{2}=-4}\end{array}\right.$.
故经过E,F两点的一次函数的解析式为y=$\frac{1}{4}$x-4.
点评 考查了反比例函数综合题,解题的关键是思路掌握待定系数法求反比例函数的解析式,待定系数法求一次函数的解析式,中点坐标公式,相似三角形的性质的知识,综合性较强,难度中等.

| A. | 4 | B. | 9 | C. | 5 | D. | 6 |
| A. | 2$\sqrt{2}$和$\sqrt{\frac{1}{2}}$ | B. | $\sqrt{2}$和$\sqrt{{2}^{2}}$ | C. | $\sqrt{{a}^{2}b}$与$\sqrt{a{b}^{2}}$ | D. | $\sqrt{4a}$与$\sqrt{2{a}^{2}}$ |
| A. | $\sqrt{2}-2\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}-\sqrt{12}$ |
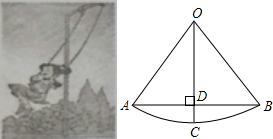 如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.
如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为0.5米.