题目内容
17.当a=3,b=2时,($\sqrt{\frac{1}{a}}$-$\sqrt{b}$)$\sqrt{ab}$的值为( )| A. | $\sqrt{2}-2\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}-\sqrt{12}$ |
分析 先利用二次根式的乘法法则运算得到原式=$\sqrt{b}$-b$\sqrt{a}$,然后把a和b的值代入即可.
解答 解:原式=$\sqrt{\frac{1}{a}•ab}$-$\sqrt{b•ab}$
=$\sqrt{b}$-b$\sqrt{a}$,
当a=3,b=2时,原式=$\sqrt{2}$-2$\sqrt{3}$.
故选A.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
12.下列说法不正确的是( )
| A. | $\sqrt{a}$(a≥0)是二次根式 | B. | 当a<0时,($\sqrt{a}$)2=-a | ||
| C. | $\sqrt{{a}^{2}+b}$是最简二次根式 | D. | $\sqrt{(x+3)^{2}}$=x+3成立的条件是x>-3 |
9.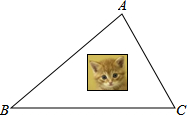 如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
 如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )| A. | △ABC三边垂直平分线的交点 | B. | △ABC三条角平分线的交点 | ||
| C. | △ABC三条高所在直线的交点 | D. | △ABC三条中线的交点 |
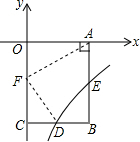 如图,已知B(4,-6),BA⊥x轴于点A,BC⊥y轴于点C,双曲线y=$\frac{k}{x}$(x>0)经过BC的中点D,且与AB交于点E.
如图,已知B(4,-6),BA⊥x轴于点A,BC⊥y轴于点C,双曲线y=$\frac{k}{x}$(x>0)经过BC的中点D,且与AB交于点E.