题目内容
5. 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2,将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y=$\frac{k}{x}$的图象上,得矩形A′B′C′D′,则反比例函数的解析式为y=$\frac{3}{2x}$.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2,将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y=$\frac{k}{x}$的图象上,得矩形A′B′C′D′,则反比例函数的解析式为y=$\frac{3}{2x}$.
分析 由四边形ABCD是矩形,得到AB=CD=1,BC=AD=2,根据A(-3,$\frac{3}{2}$),AD∥x轴,即可得到B(-3,$\frac{1}{2}$),C(-1,$\frac{1}{2}$),D(-1,$\frac{3}{2}$);根据平移的性质将矩形ABCD向右平移m个单位,得到A′(-3+m,$\frac{3}{2}$),C(-1+m,$\frac{1}{2}$),由点A′,C′在在反比例函数y=$\frac{k}{x}$(x>0)的图象上,得到方程$\frac{3}{2}$(-3+m)=$\frac{1}{2}$(-1+m),即可求得结果.
解答 解:∵四边形ABCD是矩形,
∴AB=CD=1,BC=AD=2,
∵A(-3,$\frac{3}{2}$),AD∥x轴,
∴B(-3,$\frac{1}{2}$),C(-1,$\frac{1}{2}$),D(-1,$\frac{3}{2}$);
∵将矩形ABCD向右平移m个单位,
∴A′(-3+m,$\frac{3}{2}$),C(-1+m,$\frac{1}{2}$),
∵点A′,C′在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴$\frac{3}{2}$(-3+m)=$\frac{1}{2}$(-1+m),
解得:m=4,
∴A′(1,$\frac{3}{2}$),
∴k=$\frac{3}{2}$,
∴反比例函数的解析式为:y=$\frac{3}{2x}$.
故答案为y=$\frac{3}{2x}$.
点评 本题考查了矩形的性质,图形的变换-平移,反比例函数图形上点的坐标特征,求反比例函数的解析式,掌握反比例函数图形上点的坐标特征是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
16.下列合并同类项中正确的是( )
| A. | x+2y=3xy | B. | 3xy2-3y2x=0 | C. | 4x2-2x2=2 | D. | y2+y2=2y4 |
17. 线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )
线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )
 线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )
线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )| A. | (7,2) | B. | (3.5,4) | C. | (3.5,2) | D. | (7,4) |
 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,AD=4,求AB的长.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,AD=4,求AB的长.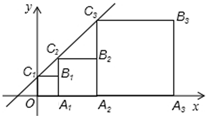 正方形OA1B1C1、正方形A1A2B2C2和正方形A2A3B3C3按如图所示方式放置,点C1、C2、C3在直线y=x+1上,点A1、A2、A3在x轴上,已知C1点的坐标是(0,1),则B3的坐标为(7,4).
正方形OA1B1C1、正方形A1A2B2C2和正方形A2A3B3C3按如图所示方式放置,点C1、C2、C3在直线y=x+1上,点A1、A2、A3在x轴上,已知C1点的坐标是(0,1),则B3的坐标为(7,4).