题目内容
15.函数[x]称为高斯函数,它表示不超过x的最大整数,例如[5.3]=5,[-2.4]=-3,[4]=4.对任意的实数x,x-1<[x]≤x.(1)证明:对于任意实数x,有[x]+[x+$\frac{1}{2}$]=[2x];
(2)解方程:[$\frac{5+6x}{8}$]=$\frac{15x-7}{5}$.
分析 (1)分别利用:①若x为整数,②若x不为整数,分析得出等式成立;
(2)首先得出$\frac{5+6x}{8}$-1<[$\frac{5+6x}{8}$]≤$\frac{5+6x}{8}$,进而得出求出x的值.
解答 (1)证明:①若x为整数,则[x]+[x+$\frac{1}{2}$]=x+x=2x=[2x];
②若x不为整数,设整数部分为a,小数部分为r(0<r<1),
当0<r<0.5时,此时0<2r<1,[x]+[x+$\frac{1}{2}$]=“a+a=<r<0.5,
[x]+[x+$\frac{1}{2}$]=[a]+[a]=2a,[2x]=[2a+2r]=2a,所以[x]+[x+$\frac{1}{2}$]=[2x],
当0.5≤r<1时,此时1≤2r<2,
[x]+[x+$\frac{1}{2}$]=a+a+1=2a+1,[2x]=[2a+2r]=2a+1,
所以[x]+[x+$\frac{1}{2}$]=[2x],
综上得:对任意的实数x有[x]+[x+$\frac{1}{2}$]=[2x];
(2)解:∵x-1<[x]≤x,
∴$\frac{5+6x}{8}$-1<[$\frac{5+6x}{8}$]≤$\frac{5+6x}{8}$,
即$\frac{5+6x}{8}$-1<$\frac{15x-7}{5}$≤$\frac{5+6x}{8}$,
解得:$\frac{41}{90}$<x≤$\frac{81}{90}$,
∴$\frac{696}{720}$≤$\frac{5+6x}{8}$≤$\frac{936}{720}$,
∴[$\frac{5+6x}{8}$]=0或1,
则$\frac{15x-7}{5}$]=0或1,
解得:x=$\frac{7}{15}$或x=$\frac{4}{5}$,
经检验都符合题意.
点评 此题主要考查了取整计算以及不等式的解法等知识,利用分类讨论得出是解题关键.


| A. | 425 | B. | 426 | C. | 427 | D. | 428 |
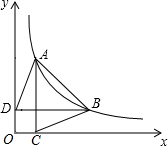 如图,已知双曲线y=$\frac{k}{x}$(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
如图,已知双曲线y=$\frac{k}{x}$(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则: