题目内容
15．已知⊙O的半径为3cm，圆心O到直线a的距离为2cm，则直线a与⊙O的位置关系为（ ）| A． | 相离 | B． | 外切 | C． | 相交 | D． | 内切 |
分析 已知圆的半径为r，圆心到直线的距离为d，那么：当d＞r时，直线与圆相离，当d=r时，直线与圆相切，当d＜r时，直线与圆相交，根据以上内容判断即可．
解答 解：∵⊙0的半径为3cm，点O到直线a的距离为2cm，
3＞2，
∴⊙O与直线a的位置关系是相交，
故选C．
点评 本题考查了直线和圆的位置关系的应用，能熟记直线和圆的位置关系内容是解此题的关键，注意：直线和圆有三种位置关系：相离，相交，相切，已知：圆的半径为r，圆心到直线的距离为d，当d＞r时，直线与圆相离，当d=r时，直线与圆相切，当d＜r时，直线与圆相交．
练习册系列答案
一本好题口算题卡系列答案
相关题目
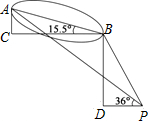有“小蛮腰”之称的广州电视塔为中国第一高电视塔，其主体顶部450～454米处有世界最高摩天轮（即图中AC=4米），与一般竖立的摩天轮不一样，广州塔的摩天轮沿着倾斜的轨道运转，对地倾斜角为∠ABC=15.5°．小明操作无人机观察摩天轮，由于设备限制无法近距离拍摄，无人机在图中P点观察到摩天轮最低点B的仰角为∠BPD=60°，最高点A的仰角为∠APD=36°，请问此时无人机距离电视塔的水平距离PD为（ ）（参考数据：tan15.5°≈0.4，tan36°≈0.7，$\sqrt{3}$≈1.7）
3．三边长均为整数且周长为24的三角形的个数为（ ）
| A． | 11 | B． | 12 | C． | 17 | D． | 18 |
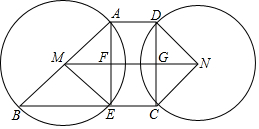如图，已知四边形BCNM是平行四边形，分别以M，N为圆心，以MB，NC为半径作圆，⊙M交BC于E，AB为⊙M的直径，连接AE交MN于F，过C点作MN的垂线MN于G，交⊙N于D，连接DN．
4．
实数a，b在数轴上的位置如图，化简$\sqrt{（a-b）^{2}}$-$\frac{a（a+b）}{|a+b|}$的结果为（ ）
实数a，b在数轴上的位置如图，化简$\sqrt{（a-b）^{2}}$-$\frac{a（a+b）}{|a+b|}$的结果为（ ）| A． | b | B． | -b | C． | -2a+b | D． | 2a-b |