题目内容
7.先化简,再求值$\frac{{{x^2}-{y^2}}}{{{x^2}-2xy+{y^2}}}•\frac{x-y}{x+y}-\frac{x}{x-y}$,其中x=1+$\sqrt{2},y=1-\sqrt{2}$.分析 首先把第一个分式的分子、分母分解因式,计算分式的乘法,然后通分、计算分式的减法即可化简,最后代入数值计算.
解答 解:原式=$\frac{(x+y)(x-y)}{(x-y)^{2}}$•$\frac{x-y}{x+y}$-$\frac{x}{x-y}$
=1-$\frac{x}{x-y}$
=$-\frac{y}{x-y}$,
当x=1+$\sqrt{2}$,y=1-$\sqrt{2}$时,原式=$\frac{{2-\sqrt{2}}}{4}$.
点评 本题考查了分式的化简求值,正确对所求的分式进行通分、约分是关键.

练习册系列答案
相关题目
18.下列命题中的真命题是( )
| A. | 长度相等的弧是等弧 | B. | 相似三角形的面积比等于相似比 | ||
| C. | 正方形不是中心对称图形 | D. | 圆内接四边形的对角互补 |
15.已知⊙O的半径为3cm,圆心O到直线a的距离为2cm,则直线a与⊙O的位置关系为( )
| A. | 相离 | B. | 外切 | C. | 相交 | D. | 内切 |
12.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1、2、3、4、5,从中随机摸出一个小球,其标号小于3的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
17.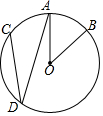 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 40° |

 如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.
如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.