题目内容
5.已知2+$\sqrt{3}$的小数部分为m,2-$\sqrt{3}$的小数部分为n,求(m+n)2015的值.分析 首先估算出$\sqrt{3}$的范围,然后可求得m、n的值,最后即可求得(m+n)2015的值.
解答 解:∵1<3<4,
∴1<$\sqrt{3}$<2.
∴m=2+$\sqrt{3}$-3=$\sqrt{3}$-1,
n=2-$\sqrt{3}$-0=2-$\sqrt{3}$,
∴(m+n)2015=12015=1.
点评 本题主要考查的是估算无理数的大小、求得m、n的值是解题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
15.已知⊙O的半径为3cm,圆心O到直线a的距离为2cm,则直线a与⊙O的位置关系为( )
| A. | 相离 | B. | 外切 | C. | 相交 | D. | 内切 |
20.下列命题是假命题的是( )
| A. | ±$\frac{1}{5}$是$\frac{1}{25}$的平方根 | B. | 81的平方根是9 | ||
| C. | 0.04的算术平方根是0.2 | D. | -27的立方根是-3 |
10.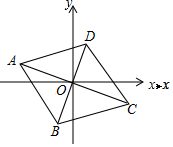 如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
 如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )| A. | (4,-2) | B. | (4,2) | C. | (2,-4) | D. | (-2,-4) |
17.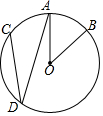 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 40° |
12.小亮玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如表所示:
若挪动n颗珠子时(n为大于1的整数)所得分数为155分,则n的值为12.
| 挪动珠子数(颗) | 2 | 3 | 4 | 5 | 6 | … |
| 所得分数 | 5 | 11 | 19 | 29 | 41 | … |