题目内容
3. 如图,在△ABC中,∠ABC=2∠C,AD是∠BAC的平分线,求证:AB+BD=AC.
如图,在△ABC中,∠ABC=2∠C,AD是∠BAC的平分线,求证:AB+BD=AC.
分析 在AC上截取AE=AB,连接DE,求出∠BAD=∠EAD,根据SAS推出△BAD≌△EAD,根据全等三角形的性质得出BD=DE,∠B=∠AED,根据三角形外角性质和已知求出∠EDC=∠C,推出DE=EC=BD即可.
解答 证明:
在AC上截取AE=AB,连接DE,
∵AD是∠BAC的平分线,
∴∠BAD=∠EAD,
∵在△BAD和△EAD中
$\left\{\begin{array}{l}{AD=AD}\\{∠BAD=∠EAD}\\{AB=AE}\end{array}\right.$
∴△BAD≌△EAD(SAS),
∴BD=DE,∠B=∠AED,
∵∠AED=∠C+∠EDC,∠B=2∠C,
∴∠EDC=∠C,
∴DE=EC=BD,
∴AB+BD=AE+EC=AC.
点评 本题考查了三角形外角性质,等腰三角形的判定,全等三角形的性质和判定的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.比较3115和769的大小关系是( )
| A. | 3115>769 | B. | 3115<769 | C. | 3115=769 | D. | 无法判定 |
12.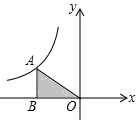 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )
 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
6.某支骨片上周末的收盘价格是每股10元.本周一到周五的收盘情况如下:
(“+”表示股票比前一天上涨,“-”表示股票比前一天下跌)
(1)这五天中哪天收盘价格最高?哪天收盘价格最低?最高与最低相差多少?
(2)买进股票时需付成交额0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税.小明哥在上周末以每股10元的价格买进2000股,然后再星期三收盘结束时将股票全部卖出,他的收益如何?
(“+”表示股票比前一天上涨,“-”表示股票比前一天下跌)
| 上周末收盘价 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 10 | +4.5 | -1.5 | +3 | -2.5 | -5 |
(2)买进股票时需付成交额0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税.小明哥在上周末以每股10元的价格买进2000股,然后再星期三收盘结束时将股票全部卖出,他的收益如何?
 如图,已知四点A,B,C,D,按照下列语句画出图形.
如图,已知四点A,B,C,D,按照下列语句画出图形.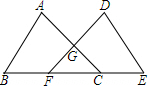 如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:
如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证: 如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE.
如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE. 某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.
某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.