题目内容
18.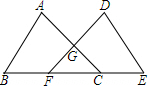 如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:
如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:(1)△ABC≌△DEF;
(2)△GFC是等腰三角形.
分析 (1)根据BE=CF得到BC=EF,然后利用SSS判定定理证明△ABC≌△DEF即可,
(2)根据全等三角形的性质得到∠ACB=∠DFE,然后由等腰三角形的判定即可得到结论.
解答 证明:(1)∵BE=CF,
∴BF+CF=CE+CF,
∴BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴GF=GC,
∴△GFC是等腰三角形.
点评 本题考查了全等三角形的判定和性质,等腰三角形的判定,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,将1,$\sqrt{2},\sqrt{3}$,$\sqrt{6}$按照如图方式排列,若规定(m,n)表示第m排从左向右的第n个数,则(15,7)表示的数是$\sqrt{6}$.
如图,将1,$\sqrt{2},\sqrt{3}$,$\sqrt{6}$按照如图方式排列,若规定(m,n)表示第m排从左向右的第n个数,则(15,7)表示的数是$\sqrt{6}$.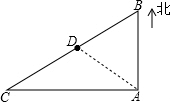 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏.
如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏. 如图,在△ABC中,∠ABC=2∠C,AD是∠BAC的平分线,求证:AB+BD=AC.
如图,在△ABC中,∠ABC=2∠C,AD是∠BAC的平分线,求证:AB+BD=AC.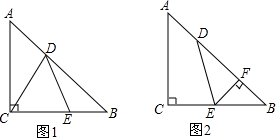
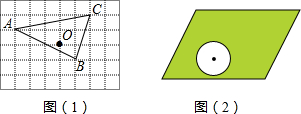
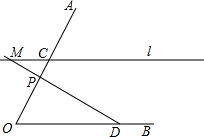 如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.
如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.