5.若函数f(x)=2x2-ax+3有一个零点为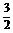 ,则f(1)=
.
,则f(1)=
.
答案 0

例1 判断下列函数在给定区间上是否存在零点.
(1)f(x)=x2-3x-18,x∈[1,8];
(2)f(x)=x3-x-1,x∈[-1,2];
(3)f(x)=log2(x+2)-x,x∈[1,3].
解(1)方法一 因为f(1)=-20<0,f(8)=22>0,
所以f(1)·f(8)<0,故f(x)=x2-3x-18,x∈[1,8]存在零点.
方法二 令x2-3x-18=0,解得x=-3或6,
所以函数f(x)=x2-3x-18,x∈[1,8]存在零点.
(2)∵f(-1)=-1<0,f(2)=5>0,
∴f(x)=x3-x-1,x∈[-1,2]存在零点.
(3)∵f(1)=log2(1+2)-1>log22-1=0.
f(3)=log2(3+2)-3<log28-3=0.∴f(1)·f(3)<0
故f(x)=log2(x+2)-x在x∈[1,3]上存在零点.
例2 求函数y=lnx+2x-6的零点个数.
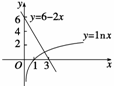 解 在同一坐标系画出y=lnx与y=6-2x的图象,
解 在同一坐标系画出y=lnx与y=6-2x的图象,
由图可知两图象只有一个交点,
故函数y=lnx+2x-6只有一个零点.
例3 (12分)(1)若函数f(x)=ax2-x-1有且仅有一个零点,求实数a的值;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
解(1)若a=0,则f(x)=-x-1,
令f(x)=0,即-x-1=0,得x=-1,故符合题意; 2分
若a≠0,则f(x)=ax2-x-1是二次函数,
故有且仅有一个零点等价于Δ=1+4a=0,
解得a=-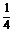 , 4分
, 4分
综上所述a=0或a=-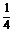 .
6分
.
6分
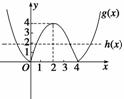 (2)若f(x)=|4x-x2|+a有4个零点,
(2)若f(x)=|4x-x2|+a有4个零点,
即|4x-x2|+a=0有四个根,即|4x-x2|=-a有四个根. 8分
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)的图象,由图象可知如果要使|4x-x2|=-a有四个根,
那么g(x)与h(x)的图象应有4个交点. 10分
故需满足0<-a<4,即-4<a<0.
∴a的取值范围是(-4,0). 12分
例4 用二分法求函数f(x)=x3-x-1在区间[1,1.5]内的一个零点(精确度0.1).
解 由于f(1)=1-1-1=-1<0,f(1.5)=3.375-1.5-1=0.875>0,
∴f(x)在区间[1,1.5]上存在零点,
取区间[1,1.5]作为计算的初始区间,
用二分法逐次计算列表如下:
|
l
端(中)点 l 坐标 |
l
中点函数值 l 符号 |
l
零点所在区间 |
l
|an-bn| |
|
l
|
l
|
l
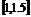 |
l
0.5 |
|
l
1.25 |
l
f(1.25)<0 |
l
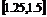 |
l
0.25 |
|
l
1.375 |
l
f(1.375)>0 |
l
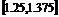 |
l
0.125 |
|
l
1.312 5 |
l
f(1.312 5)<0 |
l
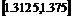 |
l
0.062 5 |
∵|1.375-1.312 5|=0.062 5<0.1,
∴函数的零点落在区间长度小于0.1的区间[1.312 5,1.375]内,故函数零点的近似值为1.312 5.

 D.
D.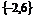
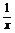 的零点所在的区间是
( )
的零点所在的区间是
( ) )
B. (
)
B. (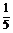 B.a≤1 C.-1≤a≤
B.a≤1 C.-1≤a≤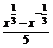 ,g(x)=
,g(x)=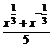 .
. 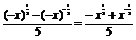 =-f(x),
=-f(x),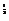 在R上递增,∴
在R上递增,∴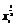 >
>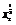 .又(x1x2)
.又(x1x2)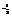 >0,
>0, 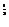 -x1
-x1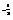 -
-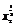 +
+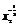 )=
)=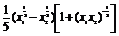 >0.
>0. 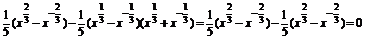 .
.
 基础自测
基础自测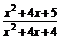 的单调区间,并比较f(-
的单调区间,并比较f(-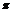 )与f(-
)与f(-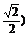 的大小.
的大小. 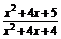 =1+
=1+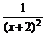 =1+(x+2)-2,其图象可由幂函数y=x-2向左平移2个单位,再向上平移1个单位,该函数在(-2,+∞)上是减函数,在(-∞,-2)上是增函数,且其图象关于直线x=-2对称(如图).
=1+(x+2)-2,其图象可由幂函数y=x-2向左平移2个单位,再向上平移1个单位,该函数在(-2,+∞)上是减函数,在(-∞,-2)上是增函数,且其图象关于直线x=-2对称(如图).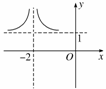 又∵-2-(-
又∵-2-(-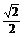 -(-2)=2-
-(-2)=2-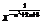 (n=2k,k∈Z)的图象在[0,+∞)上单调递增,解不等式f(x2-x)>f(x+3).
(n=2k,k∈Z)的图象在[0,+∞)上单调递增,解不等式f(x2-x)>f(x+3). 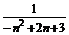 >0,
>0, 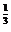 .∴f(x)在R上单调递增.
.∴f(x)在R上单调递增. 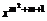 (m∈N)的定义域、值域,并判断其单调性.
(m∈N)的定义域、值域,并判断其单调性. 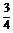 >0,
>0,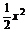 -
- ,其中在D上封闭的是
.(填序号即可)
,其中在D上封闭的是
.(填序号即可)