14.(06上海20)要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.
|
启动加速度a1 |
4 m/s2 |
|
制动加速度a2 |
8 m/s2 |
|
直道最大速度v1 |
40 m/s |
|
弯道最大速度v2 |
20 m/s |
|
直道长度 s |
218 m |
某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1=40 m/s,然后再减速到
v2=20 m/s,t1=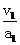 =…;t2=
=…;t2=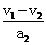 =…;t=t1+t2
=…;t=t1+t2
你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
答案 不合理 11 s
解析 上述解法不合理,因为加速时间t1=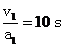 ,减速时间t2=
,减速时间t2= ,所以加速距离s1=
,所以加速距离s1= ,减速距离s2=
,减速距离s2=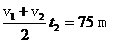 ,又因s1+s2>s,故解法不合理.
,又因s1+s2>s,故解法不合理.
摩托车先以a1=4 m/s2加速到最大速度vm,又以加速度a2=8 m/s2减速到v 2=20 m/s,恰完成直道s=218 m的距离,这样用时最短.则:加速距离s1=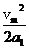 ,减速距离s2=
,减速距离s2=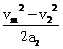
所以:
代入数据得:vm =36 m/s
加速时间t1=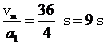
减速时间t2=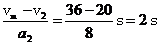
故最短时间t=t1+t2=9 s+2 s=11 s
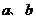 两点,相距
两点,相距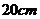 ,一质点在一恒定的合外力作用下沿
,一质点在一恒定的合外力作用下沿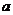 向
向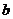 做直线运动,经过
做直线运动,经过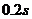 的时间先后通过
的时间先后通过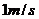 ,若力的方向由
,若力的方向由 1(2009届山东实验中学高三模拟)
在2008北京奥运会中,牙买加选手博尔特是一公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌。关于他在这两次决赛中的运动情况,下列说法正确的是 (.C )
1(2009届山东实验中学高三模拟)
在2008北京奥运会中,牙买加选手博尔特是一公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌。关于他在这两次决赛中的运动情况,下列说法正确的是 (.C )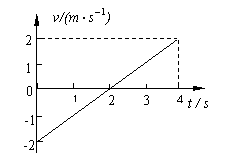 (2009广东肇庆市一模)下列运动情况可能出现的是(ABD )
(2009广东肇庆市一模)下列运动情况可能出现的是(ABD )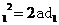 ③
③ 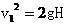 ④
④ 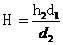
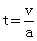 ①
①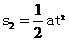 ②
②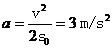
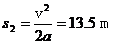
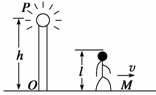 (04广西14)一路灯距地面的高度为h,身高为l的人以速度v匀速行走,
(04广西14)一路灯距地面的高度为h,身高为l的人以速度v匀速行走,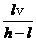
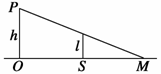 过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置,如图所示,OM为人头顶影子到O点的距离,由几何关系,有
过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置,如图所示,OM为人头顶影子到O点的距离,由几何关系,有 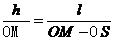 ②
②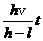 ③
③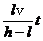
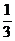 km/s.
km/s.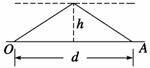 解析 如右图所示, A表示爆炸处,O表示观测者所在处,h表示地面与云层下表
解析 如右图所示, A表示爆炸处,O表示观测者所在处,h表示地面与云层下表 ②
② 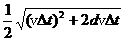
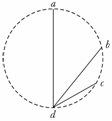 (04全国卷Ⅰ15)如图所示, ad、bd、cd是竖直面内三根固定的光滑细杆,a、b、c、d
(04全国卷Ⅰ15)如图所示, ad、bd、cd是竖直面内三根固定的光滑细杆,a、b、c、d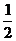 at2知d sin α=
at2知d sin α=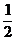 gsinα·t2
gsinα·t2