1建筑工地上一堆圆木,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根圆木?如何用简便的方法

三探究发现
变式:
问题1若把问题变成求:1+2+3+4+‥ ‥ +99=?可以用哪些方法求出来呢?
方法1:原式=(1+2+3+4+‥ ‥ +99+100)-100
方法2:原式=(1+2+3+4+‥ ‥ +98)+99
方法3:原式=0+1+2+3+4+‥ ‥ +98+99
方法4:原式=(1+2+3+4+‥ +49+51+52+‥ 99)+50
方法5:原式=(1+2+3+4+‥ ‥ +98+99+99+98+‥ +2+1)÷ 2
方法6 令 S=1+2+3+4+‥ ‥ +99
又 S=99+98+97+‥ +2+1
故 2S=(1+99)+(2+98)+‥ ‥ +(98+2)+(99+1) 从而 S =(100×99)÷ 2 = 4950
问题2:1+2+3+4+‥ ‥ +(n-1)+n=? 在上面6种方法中,哪个能较好地推广应用于这个式子的求和?
令 Sn =1+2+3+4+‥ ‥ +n,
则 Sn =n+(n-1)+‥ ‥ +2+1
从而有
2Sn =(n+1) + (n+1) + (n+1) +‥ ‥ +(n+1)
=(n+1)n

上述求解过程带给我们什么启示?
(1)所求的和可以用首项、末项及项数来表示;
(2)等差数列中任意的第k项与倒数第k项的和都等于首项与末项的和。
问题 3:现在把问题推广到更一般的情形:
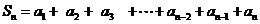 设数列 {an }为等差数列,它的首项为a1
, 公差为d, 试求 Sn =a1 +a2 + a3 +‥ ‥ + an-1 +an
设数列 {an }为等差数列,它的首项为a1
, 公差为d, 试求 Sn =a1 +a2 + a3 +‥ ‥ + an-1 +an
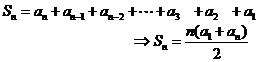
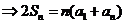 (I)
(I)
an=a1+(n-1)d代入公式(1)得
Sn=na1+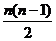 d(II)
d(II)
等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表:
|
a1 |
d |
n |
an |
sn |
|
5 |
10 |
10 |
|
|
|
|
-2 |
50 |
|
2550 |
|
-38 |
|
|
-10 |
-360 |
|
14.5 |
|
26 |
32 |
|
说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。
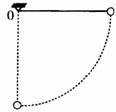 (09·广东文科基础·58) 如图8所示,用一轻绳系一小球悬于O点。现将小球拉至水 平位置,然后释放,不计阻力。小球下落到最低点的过程中,下列表述正确的是 ( A )
(09·广东文科基础·58) 如图8所示,用一轻绳系一小球悬于O点。现将小球拉至水 平位置,然后释放,不计阻力。小球下落到最低点的过程中,下列表述正确的是 ( A )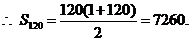 解:由题意知,这个V型架自下而上是个由120层的铅笔构成的等差数列,记为{an},
解:由题意知,这个V型架自下而上是个由120层的铅笔构成的等差数列,记为{an},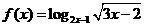 的定义域.
的定义域. 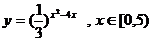 的值域.
的值域. 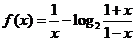 ,求函数的定义域,并讨论它的奇偶性单调性.
,求函数的定义域,并讨论它的奇偶性单调性.