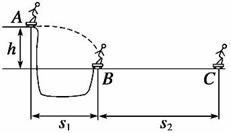
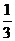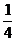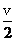8.(05·上海·19)A.某滑板爱好者在离地h=1.8 m高的平台上滑行,水平离开A点后落在水平地面的B点,其水平位移s1=3 m.着地时由于存在能量损失,着地后速度变为v=4 m/s,并以此为初速沿水平地面滑s2=8 m后停止.已知人与滑板的总质量m=60 kg。求:
(1)人与滑板在水平地面滑行时受到的平均阻力大小;
(2)人与滑板离开平台时的水平初速度.(空气阻力忽略不计,g取10 m/s2)
答案 (1)60 N? (2)5 m/s
解析 (1)设滑板在水平地面滑行时受到的平均阻力为f,
根据动能定理有-fs2=0-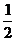 mv2 ①
mv2 ①
由①式解得f= =
=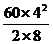 N=60N ②
N=60N ②
(2)人和滑板一起在空中做平抛运动,设初速为v0,飞行时间为t,根据平抛运动规律有
h=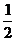 gt2 ③
gt2 ③
v0=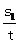 ④
④
由③④两式解得
v0= =
=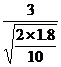 m/s=5 m/s
m/s=5 m/s
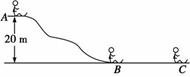 B.如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止,人与雪橇的总质量为70 kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:
B.如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止,人与雪橇的总质量为70 kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:
|
位置 |
A |
B |
C |
|
速度(m/s) |
2.0 |
12.0 |
0 |
|
时刻(s) |
0 |
4 |
10 |
(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力大小.(g取10 m/s2)
答案 (1)9 100 J (2)140 N?
解析 (1)从A到B的过程中,人与雪橇损失的机械能为
? ΔE=mgh+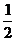 mvA2-
mvA2-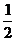 mvB2
mvB2
? =(70×10×20+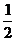 ×70×2.02-
×70×2.02-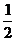 ×70×12.02)J=9 100 J
×70×12.02)J=9 100 J
(2)人与雪橇在BC段做匀减速运动的加速度
a= =
=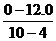 m/s2=-2 m/s2
m/s2=-2 m/s2
根据牛顿第二定律
f=ma=70×(-2) N=-140 N
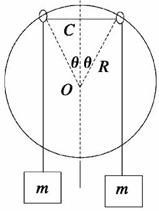 (04·江苏·15)如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上.一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小。
(04·江苏·15)如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上.一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小。 的位置上(如图).在两个小圆
的位置上(如图).在两个小圆 m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略.求重物M下降的最大距离;
m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略.求重物M下降的最大距离;
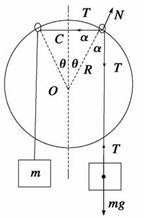 解析 ⑴重物向下先做加速运动、后做减速运动,当重物速度为零时,下降的距离最大,设下降的最大距离为h,由机械能守恒定律得 Mgh=2mg[
解析 ⑴重物向下先做加速运动、后做减速运动,当重物速度为零时,下降的距离最大,设下降的最大距离为h,由机械能守恒定律得 Mgh=2mg[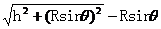 ] 解得 h=
] 解得 h=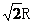
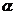 角的位置上(如图
角的位置上(如图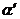 得
得 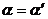 ,而,所以
,而,所以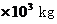 的客机,从静止开始沿平直的跑道滑行,当滑行距离:s=7.2
的客机,从静止开始沿平直的跑道滑行,当滑行距离:s=7.2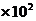 m时,达到起飞的速度v=60 m/s.
m时,达到起飞的速度v=60 m/s.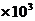 N,牵引力与第⑵问中求得的值相等,则要达到上述起飞速度,飞机的滑行距离应为多大?
N,牵引力与第⑵问中求得的值相等,则要达到上述起飞速度,飞机的滑行距离应为多大?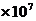 J ⑵1.5
J ⑵1.5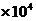 N ⑶
N ⑶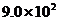 m
m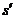 ,由动能定理,得(F1-F)
,由动能定理,得(F1-F)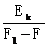 ,代入数值得
,代入数值得 m
m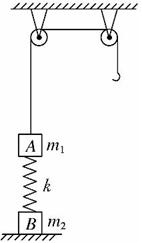
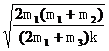
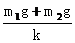 ①
① 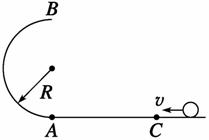
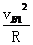 ,vB1=2 m/s ②
,vB1=2 m/s ② 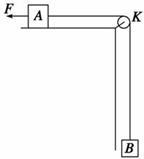
 是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求: 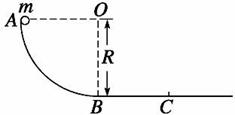
 mv2=
mv2=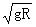
 ,mgR=
,mgR= (05·江苏·10)如图所示, 固定的光滑竖直杆上套着一个滑块,用轻绳系着滑块绕过光滑的定滑轮,以大小恒定的拉力F拉绳,使滑块从A点起由静止开始上升.若从A点上升至B点和从B点上升至C点的过程中拉力F做的功分别为W1、W2,滑块经B、C两点时的动能分别为EkB、EkC,图中AB=BC,则一定
(
)
(05·江苏·10)如图所示, 固定的光滑竖直杆上套着一个滑块,用轻绳系着滑块绕过光滑的定滑轮,以大小恒定的拉力F拉绳,使滑块从A点起由静止开始上升.若从A点上升至B点和从B点上升至C点的过程中拉力F做的功分别为W1、W2,滑块经B、C两点时的动能分别为EkB、EkC,图中AB=BC,则一定
(
)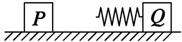 A.P的初动能
A.P的初动能