7、板书设计:
|
辗转相除法 1、分析 3、流程图 5、演板练习 2、算法 4、 伪代码 |
4、应用辗转相除法算法
[练2]右面一段伪代码的目的是:( )
A.求x,y的最小公倍数 B.求x,y的最大公约数
C.求x被y整除的商 D. 求y被x整除的商
[生答] B
[设计意图]会“ 识”直到型循环语句描述的应用辗转相除法求最大公约数。
|
A.1 B.429
C.190 D.6
[生答] A
[设计意图]会“识”当型循环语句描述辗转相除法
并且会“算”最大公约数。
[练4]设计计算两个正整数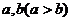 的
的
最小公倍数的算法。
[设计意图]会“用”辗转相除法的算法语句。
[师提示]最小公倍数=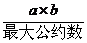
[生演板]
|
|
|
[问6]:还有其他算法吗?
[生答]运用案例1穷举算法方法
[设计意图]①巩固练习辗转相除法算法;②重温上节课孙子问题的穷举算法思想。
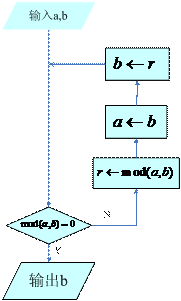
3、设计辗转相除法算法
[问4]写出两个正整数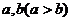 的最大公约数的一个算法。
的最大公约数的一个算法。
[师初步分析]运用辗转相除法,产生一列数: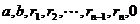 。这列数从第三项开始,每项都是前两项相除所得的余数,余数为0的前一项
。这列数从第三项开始,每项都是前两项相除所得的余数,余数为0的前一项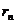 ,既是
,既是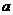 和
和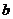 的最大公约数。
的最大公约数。
递推关系: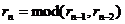 (其中
(其中 ,
, )
)
[问5]可选用什么结构书写此算法?
[生答]循环结构。
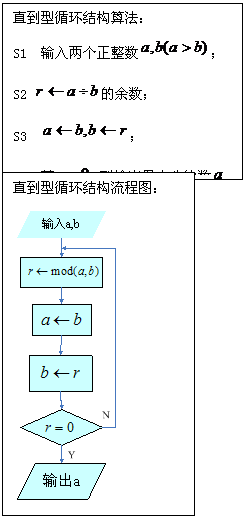
[生分组讨论]共分为两个小组,分别用直到型和当型循环结构写算法、画流程图和写伪代码,并派代表演板流程图和伪代码。
|
 |
|||
|
|
|
||||
[师点评结果]通过演板的流程图和伪代码的对比,梳理算法,
|
[设计意图]
①多角度分析问题,加强综合运用知识能力;
②通过小组合作探索,激发学生兴趣,巩固新知;
③渗透从具体到抽象的数学思想方法,体会迭代
的算法思想。

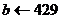

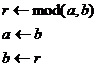
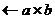


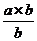




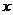
 ,则输出最大公约数b;若
,则输出最大公约数b;若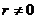 ,则转S3。
,则转S3。 的余数;
的余数;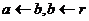 ;
;
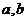
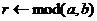

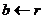
 x
x