7、 抽样方法
(1)简单随机抽样:概率 其中n为样本容量, N为个体总数
其中n为样本容量, N为个体总数
(2)分层抽样: 其中n为样本容量, N为个体总数
其中n为样本容量, N为个体总数
n1为分层样本容量, N1为分层个体总数
[题例分析]
例1:甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)求甲答对试题数ξ的概率分布及数学期望;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
解:(Ⅰ)依题意,甲答对试题数ξ的概率分布如下:

甲答对试题数ξ的数学期望
(Ⅱ)设甲、乙两人考试合格的事件分别为A、B,则

因为事件A、B相互独立,
∴甲、乙两人考试均不合格的概率为

∴甲、乙两人至少有一人考试合格的概率为
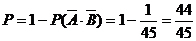
答:甲、乙两人至少有一人考试合格的概率为 .
.
例2. 某射击运动员每次射击击中目标的概率为p(0<p<1)。他有10发子弹,现对某一目标连续射击,每次打一发子弹,直到击中目标,或子弹打光为止。求他击中目标的期望。
解:射手射击次数的可能取值为1,2,…,9,10。
若 ,则表明他前
,则表明他前 次均没击中目标,而第k次击中目标;若k=10,则表明他前9次都没击中目标,而第10次可能击中也可能没击中目标。因此
次均没击中目标,而第k次击中目标;若k=10,则表明他前9次都没击中目标,而第10次可能击中也可能没击中目标。因此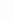 的分布列为
的分布列为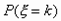



用倍差法,可求得


所以
例3 、9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为0 5,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需补种假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望
5,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需补种假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望 (精确到0
(精确到0 01)
01)
解:某坑需补种的概率为 ,不需补种的概率为
,不需补种的概率为

 的分布列为:
的分布列为:
|
ξ |
0 |
10 |
20 |
30 |
|
P |
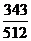 |
 |
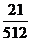 |
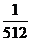 |
∴Eξ=0×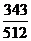 +10×
+10× +20×
+20×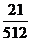 +30×
+30×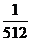 =3
=3 75
75
例4、.有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数较大者获胜
⑴分别求出两只骰子投掷所得点数的分布列及期望;
⑵投掷蓝色骰子者获胜的概率是多少?
⒙解:⑴红色骰子投掷所得点数为 是随即变量,其分布如下:
是随即变量,其分布如下:

 8 2
8 2
P 
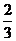
E =8·
=8· +2·
+2·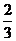 =4
=4
蓝色骰子投掷所得点数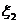 是随即变量,其分布如下:
是随即变量,其分布如下:

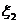 7 1
7 1
P 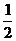
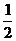
E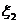 =7·
=7·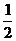 +1·
+1·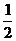 =4
=4
[巩固训练]
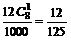 .
. ,故其中至少有一个面上涂有红色的概率为P=1-
,故其中至少有一个面上涂有红色的概率为P=1-


 即为所求。
即为所求。 即为所求。
即为所求。
 变形为:
变形为:

 应取什么特殊值:
应取什么特殊值:

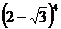 =
=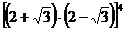 =1
=1 =
= ,而
,而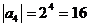 所以,
所以, =
= 为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:(1) 每次抽取的产品都不放回到这批产品中的
为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:(1) 每次抽取的产品都不放回到这批产品中的 的期望、方差、标准差分别是多少?
的期望、方差、标准差分别是多少?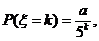 a为常数,k=1,2,、、、,则a=
a为常数,k=1,2,、、、,则a=
 (2)ξ-B(n,p),则Dξ=np(1-p).
(2)ξ-B(n,p),则Dξ=np(1-p).