2.重点公式
(1)如果事件A、B互斥,那么事件A+B发生(即A、B中有一个发生)的概率,等于事件A、B分别发生的概率和,即P(A+B)=P(A)+P(B),推广:P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
(2)对立事件的概率和等于1.
P(P)+P(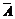 )=P(A+
)=P(A+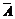 )=1.
)=1.
[题例分析]
例1、甲、乙二人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个.甲、乙二人各抽一题:
(1)求甲抽到选择题,乙抽到判断题的概率;
(2)求甲、乙两人中至少一人抽到选择题的概率.
解:(1)甲抽到选择题、乙抽到判断题的可能结果有C ·C
·C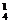 个,又甲、乙依次抽到一题的可能结果有C
个,又甲、乙依次抽到一题的可能结果有C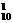 C
C 个,所以,所求概率为:
个,所以,所求概率为: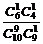 =
=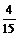 .
.
(2)甲、乙二人依次都抽到判断题的概率为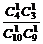 ,故甲、乙二人中至少有一人抽到选择题的概率为:1-
,故甲、乙二人中至少有一人抽到选择题的概率为:1-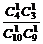 =1-
=1-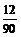 =1-
=1-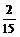 =
= .
.
例2、某射手在一次射击中命中9环的概率是0.28,命中8环的概率是0.19,不够8环的概率是0.29.计算这个射手在一次射击中命中9环或10环的概率.
解:设这个射手在一次射击中命中10环或9环为事件A,命中10环、9环、8环以及不够8环的事件分别记为A1、A2、A3、A4.
∵A2、A3、A4彼此互斥,
∴P(A2+A3+A4)=P(A2)+P(A3)+P(A4)=0.28+0.19+0.29=0.76.
又∵A1= ,∴P(A1)=1-P(A2+A3+A4)=1-0.76=0.24.
,∴P(A1)=1-P(A2+A3+A4)=1-0.76=0.24.
∵A1与A2互斥,
∴P(A)=P(A1+A2)=P(A1)+P(A2)=0.24+0.28=0.52.
故这个射手在一次射击中命中10环或9环的概率为0.52.
例3、袋中放有3个伍分硬币,3个贰分硬币和4个壹分硬币,从中任取3个,求总值超过8分的概率.
解:记“总值超过8分”为事件A,它应有四种情况:
(1)“取到3个伍分硬币”为事件A1;
(2)“取到2个伍分和一个贰分硬币”为事件A2;
(3)“取到2个伍分和一个壹分硬币”为事件A3;
(4)“取到一个伍分硬币和2个贰分硬币”为事件A4.
则P(A1)=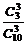 =
=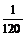 . P(A2)=
. P(A2)=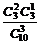 =
= .
.
P(A3)=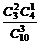 =
= . P(A4)=
. P(A4)=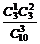 =
= .
.
依题意,A1、A2、A3、A4彼此互斥,
∴P(A)=P(A1+A2+A3+A4)=P(A1)+P(A2)+P(A3)+P(A4)=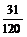
例4、经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
|
排队人数 |
0-5 |
6-10 |
11-15 |
16-20 |
21-25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(I)每天不超过20人排队结算的概率是多少?
(Ⅱ)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
解:(I)每天不超过20人排队结算的概率为:P=0.1+0.15+0.25+0.25=0.75,即不超过20人排队结算的概率是0.75.
(Ⅱ)每天超过15人排队结算的概率为:0.25+0.2+0.05=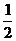 ,
,
一周7天中,没有出现超过15人排队结算的概率为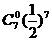 ;
;
一周7天中,有一天出现超过15人排队结算的概率为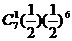 ;
;
一周7天中,有二天出现超过15人排队结算的概率为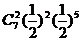 ;
;
所以有3天或3天以上出现超过15人排队结算的概率为:
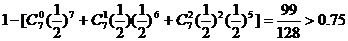 ,
,
所以,该商场需要增加结算窗口.
[巩固训练]

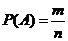 .
.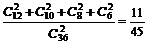 .
.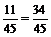 .
. ,求男、女相差几名?
,求男、女相差几名?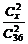 =
=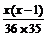 .选得两名委员都是女性的概率为
.选得两名委员都是女性的概率为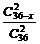 =
=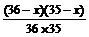 .
.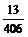 ,且n≥2,计算红球有几个?
,且n≥2,计算红球有几个?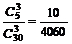 ,P(C)=
,P(C)=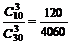 .
.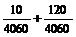 .∴P(A)=0,即取3个球,是红球的个数小于或等于2.
.∴P(A)=0,即取3个球,是红球的个数小于或等于2.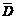 为“3个球中没有红球”,则
为“3个球中没有红球”,则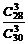 =
=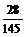 .
.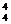 种不同方式.
种不同方式. ·A
·A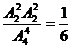 (2)第二次取出是二等品共有:
(2)第二次取出是二等品共有: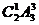 ,
,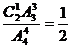
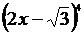 =
=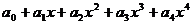 ,求(1)
,求(1) ―
― 的值。(2)
的值。(2) 的值。
的值。