0 53691 53699 53705 53709 53715 53717 53721 53727 53729 53735 53741 53745 53747 53751 53757 53759 53765 53769 53771 53775 53777 53781 53783 53785 53786 53787 53789 53790 53791 53793 53795 53799 53801 53805 53807 53811 53817 53819 53825 53829 53831 53835 53841 53847 53849 53855 53859 53861 53867 53871 53877 53885 447348
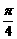 ,下列关系中正确的是( )
,下列关系中正确的是( )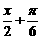 )在[p,2p]上的最小值是( )
)在[p,2p]上的最小值是( )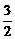 p, 则
p, 则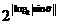 等于( )
等于( )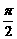 , kÎZ}
, kÎZ}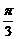 )的终边相同的角的集合是{a|a=kp-
)的终边相同的角的集合是{a|a=kp-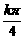 , kÎZ},
B={x|x=
, kÎZ},
B={x|x=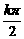 +
+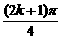 可视为
可视为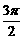 .
.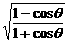 =ctgq-cscq,求q取值范围。
=ctgq-cscq,求q取值范围。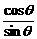 -
-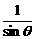 =
=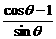 ,这样就决定了左边的变形方向。
,这样就决定了左边的变形方向。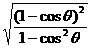 =
=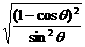 ,
,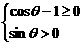 Þ
Þ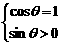 Þq无解,
Þq无解,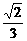 ,
, 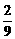 ,
,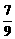 ,
,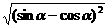 =
=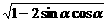 =
=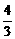 .
.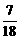 )
)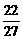 .
.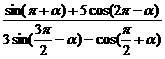 (2)1+cos2a-
(2)1+cos2a-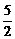 sin2a.
sin2a.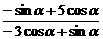 =
=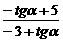 =-
=-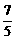 。
。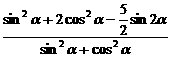 =
=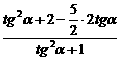
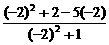 =
=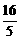 .
.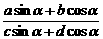 为关于sina与cosa的一次分式齐次式,处理的方法,就是将分子与分母同除以cosa,即可化为只含tga的式子。而对于1+cos2a-
为关于sina与cosa的一次分式齐次式,处理的方法,就是将分子与分母同除以cosa,即可化为只含tga的式子。而对于1+cos2a-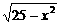 +logsinx(2sinx-1)的定义域。
+logsinx(2sinx-1)的定义域。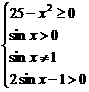 Þ
Þ 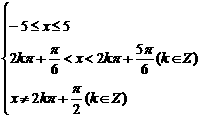

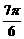 )∪(
)∪(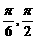 )∪(
)∪(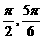 )。
)。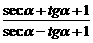 =
=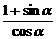 .
.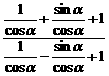 =
=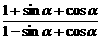
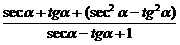
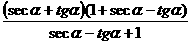 =seca+tga=
=seca+tga=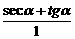 =
=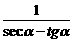 .
.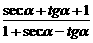 =seca+tga=
=seca+tga=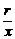 , tga=
, tga=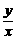 , sina=
, sina=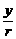 , cosa=
, cosa=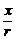 .
.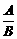 =1 (B¹0)
=1 (B¹0)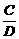 Û AD=BC
(BD¹0)
Û AD=BC
(BD¹0)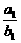 =
=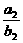 =……=
=……=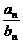 ,则
,则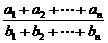 =
=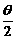 所在的象限是( )
所在的象限是( )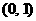 . 12.
. 12. 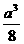 . 13.(Ⅰ)
. 13.(Ⅰ)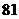 ; (Ⅱ)
; (Ⅱ) . 14.
. 14.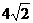 . 15.
. 15.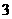 .
.