高考数学题中,最后三个大题往往是综合的知识多、技巧性强、能力要求高的综合性题目,它解答成功与否将直接影响着升学档次。大量未成功的考生并不完全是水平和能力问题,而是心理不佳、方法不当,导致宝贵的时间白白流失,发挥不出自己应有的水平,使自己无缘问鼎名校或重点大学,饮恨终身。那么面对综合试题,考生应答呢?
1. 下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
…… |
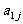 |
…… |
|
7 |
12 |
( ) |
( ) |
( ) |
…… |
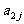 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
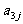 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
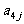 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
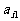 |
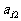 |
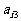 |
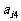 |
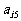 |
…… |
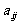 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
其中每行、每列都是等差数列,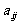 表示位于第i行第j列的数.(1)写出
表示位于第i行第j列的数.(1)写出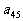 的值; (2)写出
的值; (2)写出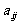 的计算公式;(3)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
的计算公式;(3)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
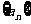 满足
满足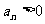 ,且对一切
,且对一切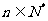 ,有
,有 ,其中
,其中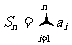 .
.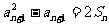 ;
;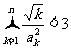 .
.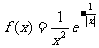 (
(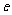 为自然对数的底数),
为自然对数的底数), 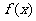 的奇偶性;
的奇偶性; 上求函数的极值;
上求函数的极值;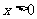 时,对任意正整数
时,对任意正整数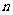 都有
都有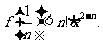

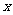 的方程
的方程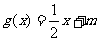 有实数根,求实数
有实数根,求实数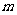 的取值集合;
的取值集合;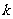 ,使得关于
,使得关于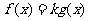 有两个不相等的实数根?如果存在,求
有两个不相等的实数根?如果存在,求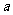 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为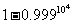 .
.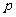 ;
;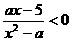 的解集为M.
的解集为M.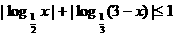
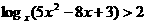
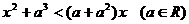
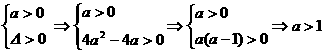 时,方程ax2+2ax+1=0有两根
时,方程ax2+2ax+1=0有两根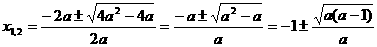 .
.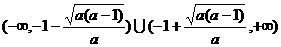 .
.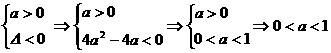 时,
时,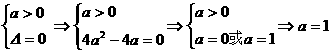 时,
时,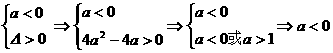 时,
时,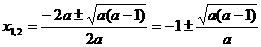
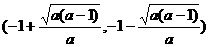 .
.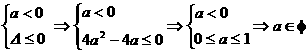
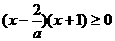 ,
,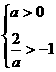 ,即a>0时,不等式解为
,即a>0时,不等式解为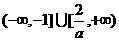 .
.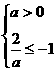 ,此时a不存在.
,此时a不存在. ,
,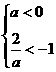 ,即-2<a<0时,不等式解为
,即-2<a<0时,不等式解为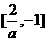
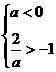 ,即a<-2时,不等式解为
,即a<-2时,不等式解为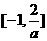 .
.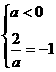 ,即a=-2时,不等式解为x=-1.
,即a=-2时,不等式解为x=-1.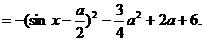
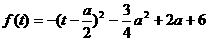 (t∈[-1,1]).
(t∈[-1,1]).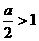 即a>2时,t=1,
即a>2时,t=1,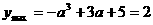
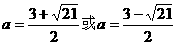 (舍).
(舍). 时,即-2≤a≤2时,
时,即-2≤a≤2时,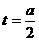 ,
,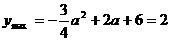 ,
,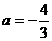 或a=4(舍).
或a=4(舍).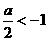 即a<-2时, t=-1时,ymax=-a2+a+5=2
即a<-2时, t=-1时,ymax=-a2+a+5=2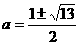 , ∵ a<-2, ∴
, ∵ a<-2, ∴ 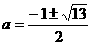 全都舍去.
全都舍去.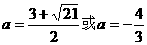 时,能使函数f(x)的最大值为2.
时,能使函数f(x)的最大值为2.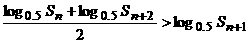 .
.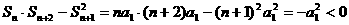
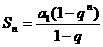 , 从而
, 从而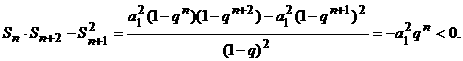
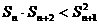 .
.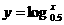 为单调递减函数.∴
为单调递减函数.∴ 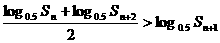 .
.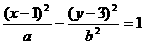 ,一条渐近线的斜率为
,一条渐近线的斜率为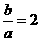 , ∴ b=2.∴
, ∴ b=2.∴ 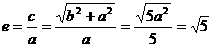 .
.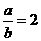 ,此时
,此时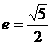 .
.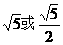 .
.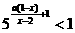 .
.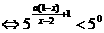
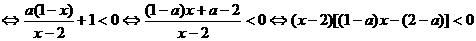
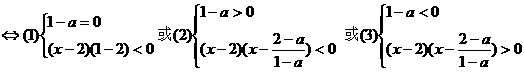
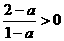 ,下面分为三种情况.
,下面分为三种情况.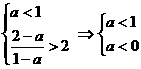 即a<1时,解为
即a<1时,解为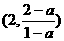 .
.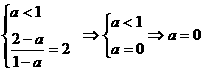 时,解为Æ.
时,解为Æ.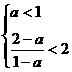 Þ
Þ 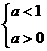 即0<a<1时,原不等式解为:
即0<a<1时,原不等式解为: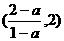 .
.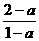 的符号不确定,也分为3种情况.
的符号不确定,也分为3种情况.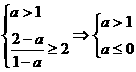 Þ a不存在.
Þ a不存在.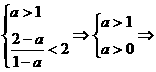 当a>1时,原不等式的解为:
当a>1时,原不等式的解为: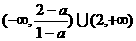 .
.