0 53672 53680 53686 53690 53696 53698 53702 53708 53710 53716 53722 53726 53728 53732 53738 53740 53746 53750 53752 53756 53758 53762 53764 53766 53767 53768 53770 53771 53772 53774 53776 53780 53782 53786 53788 53792 53798 53800 53806 53810 53812 53816 53822 53828 53830 53836 53840 53842 53848 53852 53858 53866 447348
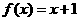 ,②
,②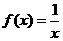 ,③
,③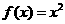 ,④
,④ ,其中在
,其中在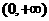 是增函数的有( )
是增函数的有( )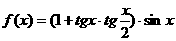 的奇偶性及周期性。
的奇偶性及周期性。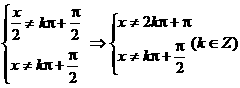
 ∴ f(x)定义域关于原点对称,如图:
∴ f(x)定义域关于原点对称,如图: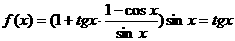
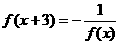 ,又当x∈[-3,-2]时,f(x)=2x,求f(113.5)的值。
,又当x∈[-3,-2]时,f(x)=2x,求f(113.5)的值。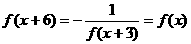 , ∴ f(x)周期T=6,
, ∴ f(x)周期T=6,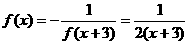 ,
,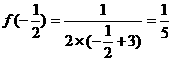 .
.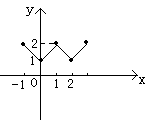 小结:由奇偶性结合周期性,将要求区间上问题转化为已知解析式的区间上。
小结:由奇偶性结合周期性,将要求区间上问题转化为已知解析式的区间上。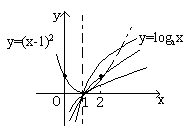 <2>已知二次函数f(x)=x2+ax+5对任意t都有f(t)=f(-4-t),且在闭区间Z[m,0]上有最大值5,最小值1,求m的取值范围。
<2>已知二次函数f(x)=x2+ax+5对任意t都有f(t)=f(-4-t),且在闭区间Z[m,0]上有最大值5,最小值1,求m的取值范围。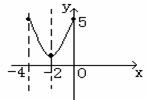 ∵ x∈[m,0], [f(x)]max=5, [f(x)]min=1,
∵ x∈[m,0], [f(x)]max=5, [f(x)]min=1,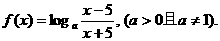
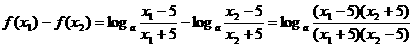 ,
,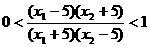 ,
,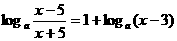 。
。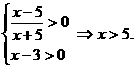
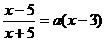 有大于5的实根。
有大于5的实根。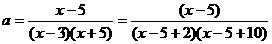 (∵ x>5)
(∵ x>5)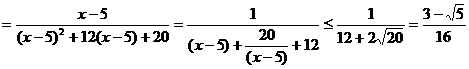
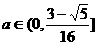 .
.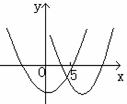 ①有一根大于5
①有一根大于5 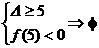 .
.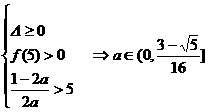 .
.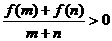 。
。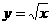 图象,经过如何变换可得下列函数图象?
图象,经过如何变换可得下列函数图象?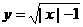 <2>
<2>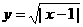
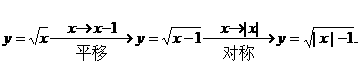
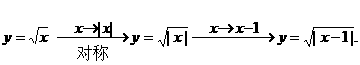
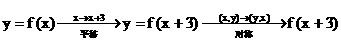 的反函数。
的反函数。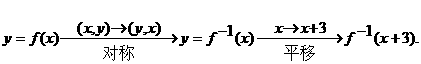
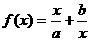 形式。注意识别及应用条件。
形式。注意识别及应用条件。