22. 解:(1) 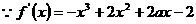
由题意可得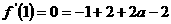
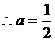 …………………2分
…………………2分
(2)由(1)知
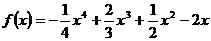
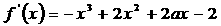 =
=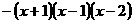
由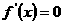 得
得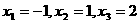
当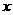 变化时,
变化时,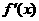 与
与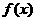 的变化情况如下表:
的变化情况如下表:
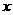 |
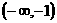 |
-1 |
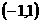 |
1 |
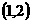 |
2 |
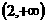 |
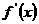 |
+ |
0 |
-- |
0 |
+ |
0 |
--- |
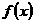 |
 |
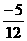 |
 |
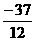 |
 |
 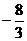 |
 |
从而可知,当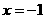 时,函数
时,函数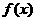 取得极大值
取得极大值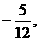
当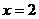 时, 函数
时, 函数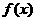 取得极大值
取得极大值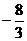 ,极小值
,极小值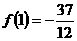
作出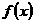 的大致图像
的大致图像
因关于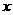 的方程
的方程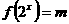 有三个不同的实数解,令
有三个不同的实数解,令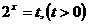 ,即关于
,即关于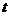 的方程
的方程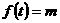 在
在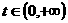 上有三个不同的实数解.即
上有三个不同的实数解.即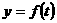 的图像与直线
的图像与直线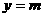 在
在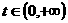 上有三个不同的交点,而
上有三个不同的交点,而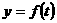 的图像与
的图像与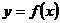 的图像一致.又有
的图像一致.又有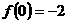 ,由图可知,
,由图可知,
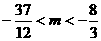 ……………………7分
……………………7分
(3)当函数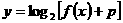 的图像与坐标轴无交点,分以下两种情况:
的图像与坐标轴无交点,分以下两种情况:
(1) 当函数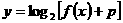 的图像与
的图像与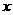 轴无交点时,则必须有
轴无交点时,则必须有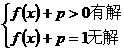 ,即
,即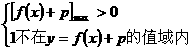 ,
,
而 函数
函数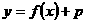 的值域为
的值域为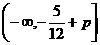 ,
,

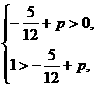 解得
解得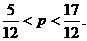
(2)当函数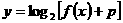 的图像与
的图像与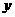 轴无交点时,则必须有
轴无交点时,则必须有
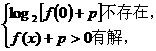 即
即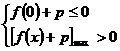 ,即
,即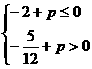
解得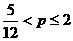 ,
,
综上, 实数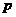 的取值范围为
的取值范围为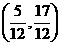 ………………….14分
………………….14分
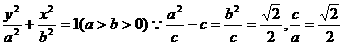
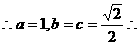 椭圆C的方程为
椭圆C的方程为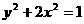 ………………4分
………………4分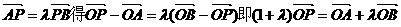
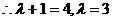 设
设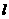 与椭圆C交点为
与椭圆C交点为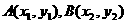
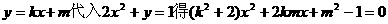
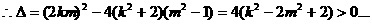 ①
①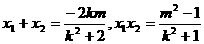
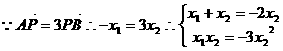
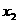 得
得 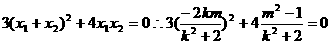
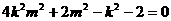
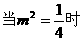
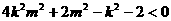
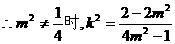 由①得
由①得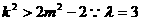
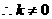
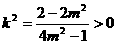
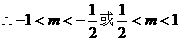
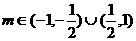 ………………………………12分
………………………………12分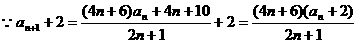
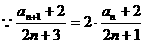
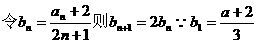
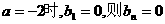
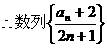 不是等比数列,
不是等比数列,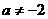 时,
时,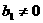 ,数列
,数列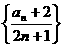 是等比数列且公比为2,………4分
是等比数列且公比为2,………4分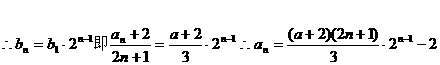 ……6分
……6分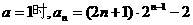
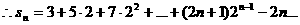 1°
1°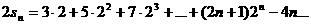 2°
2°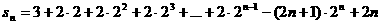
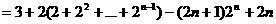
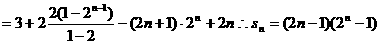 ………12分
………12分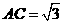 ,从而
,从而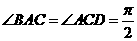 ,由三垂线定理知:
,由三垂线定理知: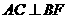 。………3分
。………3分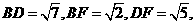 由勾股定理知
由勾股定理知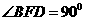 ,设点
,设点 在面
在面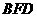 内的射影为
内的射影为 ,过
,过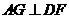 于
于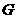 ,连结
,连结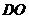 ,则
,则 为二面角
为二面角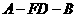 的平面角。在
的平面角。在 中由面积法易求
中由面积法易求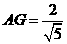 ,由体积法求得点
,由体积法求得点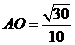 ,所以
,所以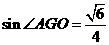 ,所以求二面角
,所以求二面角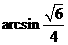 。………8分
。………8分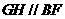 交
交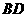 于
于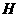 ,连结
,连结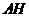 。则易证
。则易证 为二面角
为二面角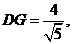 于是
于是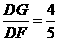 ,所以
,所以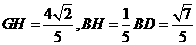 ,在
,在 中由余弦定理求得
中由余弦定理求得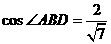 。再在
。再在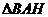 中由余弦定理求得
中由余弦定理求得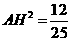 。最后在
。最后在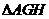 中由余弦定理求得
中由余弦定理求得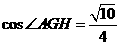 ,所以求二面角
,所以求二面角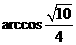 。
。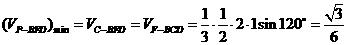 。………12分
。………12分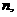 则
则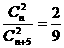 …………2分
…………2分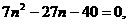
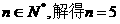 ,即有5个数学题。…6分
,即有5个数学题。…6分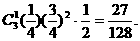 …………8分
…………8分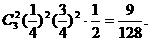 …………10分
…………10分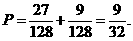 …………12分
…………12分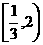 16、①④
16、①④ (本题满分14分)
(本题满分14分)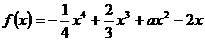 ,在区间
,在区间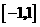 上为减函数,在区间
上为减函数,在区间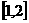 上为增函数。
上为增函数。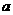 的值;
的值; 的取值范围;
的取值范围;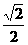 ,直线
,直线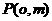 与椭圆C交于相异两点A、B且
与椭圆C交于相异两点A、B且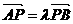 。
。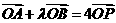 ,求
,求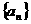 满足
满足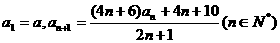
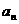 ;
;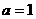 时,数列
时,数列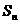 ,求
,求