(17)(本小题满分10分)
等比数列{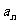 }的前n 项和为
}的前n 项和为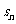 ,已知
,已知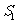 ,
,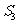 ,
,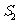 成等差数列
成等差数列
(1)求{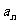 }的公比q;
}的公比q;
(2)求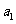 -
-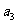 =3,求
=3,求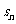
(18)(本小题满分12分)
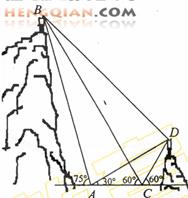
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为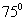 ,
,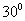 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为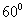 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,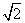
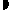 1.414,
1.414,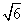
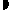 2.449)
2.449)
(19)(本小题满分12分)
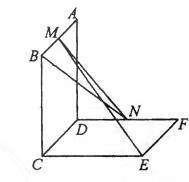
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。
(I)若CD=2,平面ABCD ⊥平面DCEF,求直线MN的长;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。
(20)(本小题满分12分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
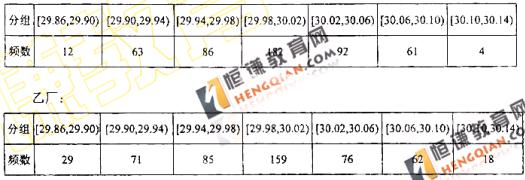
(1) 试分别估计两个分厂生产的零件的优质品率;
(2)
由于以上统计数据填下面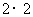 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
|
|
甲 厂 |
乙 厂 |
合计 |
|
优质品 |
|
|
|
|
非优质品 |
|
|
|
|
合计 |
|
|
|
附: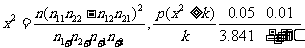
(21)(本小题满分12分)
设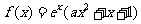 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。
(I) 求a的值,并讨论f(x)的单调性;
(II)
证明:当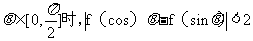
(22)(本小题满分12分)
已知,椭圆C以过点A(1,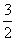 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1) 求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
 5﹜,N=﹛x|x<-5或x>5﹜,则M
5﹜,N=﹛x|x<-5或x>5﹜,则M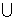 N=
N=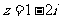 ,那么
,那么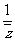 =
=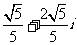 (B)
(B)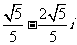 (C)
(C)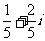 (D)
(D)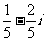
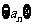 为等差数列,且
为等差数列,且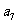 -2
-2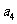 =-1,
=-1, 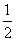 (C)
(C)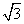 (B)2
(B)2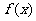 满足:x
满足:x 4,则
4,则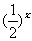 ;当x<4时
;当x<4时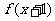 ,则
,则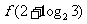 =
=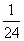 (B)
(B)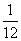 (C)
(C)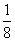 (D)
(D)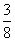
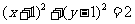 (B)
(B) 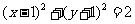
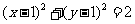 (D)
(D) 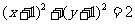

 ,。。。
,。。。 ,其中收入记为
,其中收入记为
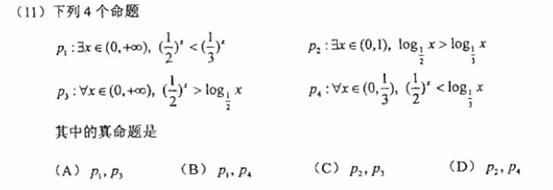
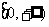 单调增加,则满足
单调增加,则满足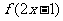 <
<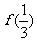 的x 取值范围是
的x 取值范围是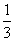 ,
,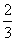 ) (B) [
) (B) [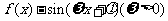 的图象如图所示,
的图象如图所示,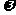 =
= 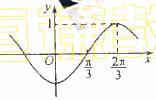
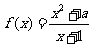 在
在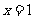 处取极值,则
处取极值,则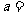
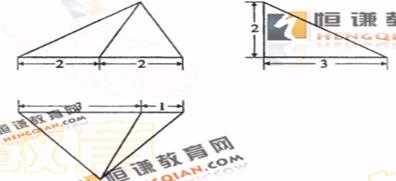
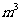
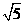 ,AC=3,sinC=2sinA
,AC=3,sinC=2sinA 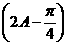 的值
的值 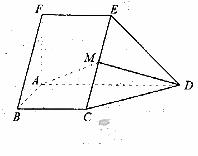 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA  平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB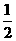 AD
AD  其中
其中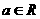
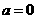 时,求曲线
时,求曲线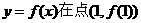 处的切线的斜率;
处的切线的斜率; 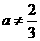 时,求函数
时,求函数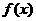 的单调区间与极值。
的单调区间与极值。 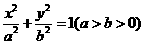 的两个焦点分别为
的两个焦点分别为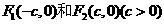 ,过点
,过点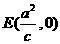 的直线与椭圆相交与
的直线与椭圆相交与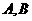 两点,且
两点,且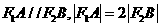 。
。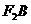 上有一点
上有一点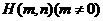 在
在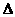
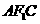 的外接圆上,求
的外接圆上,求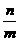 的值
的值 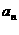 }的公差为d(d
}的公差为d(d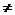 0),等比数列{
0),等比数列{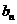 }的公比为q(q>1)。设
}的公比为q(q>1)。设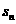 =
=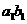 +
+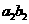 …..+
…..+ 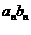 ,
,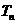 =
=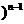

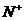
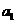 =
=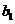 = 1,d=2,q=3,求
= 1,d=2,q=3,求 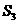 的值;
的值;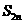 -(1+q)
-(1+q)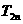 =
=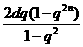 ,n
,n n
n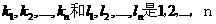 的两个不同的排列,
的两个不同的排列, 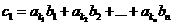 ,
, 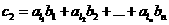 证明
证明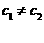 。
。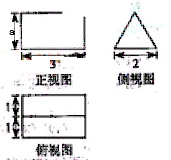 (11)某学院的A,B,C三个专业共有1200名学生,为了调
(11)某学院的A,B,C三个专业共有1200名学生,为了调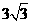 ,则
,则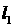 的参数方程为
的参数方程为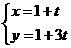 (t为参数),直线
(t为参数),直线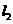 的方程为y=3x+4则
的方程为y=3x+4则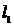 与
与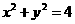 与圆
与圆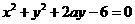 (a>0)的公共弦的长为
(a>0)的公共弦的长为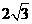 ,
,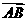 =
=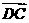 =(1,1),
=(1,1),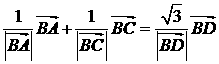 ,则四边形ABCD的面积是
,则四边形ABCD的面积是
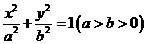 的两个焦点分别为
的两个焦点分别为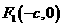 和
和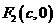 ,过点
,过点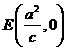 的直线与椭圆相交于
的直线与椭圆相交于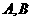 两点,且
两点,且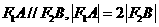
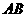 的斜率
的斜率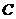 与点
与点 关于坐标原点对称,直线
关于坐标原点对称,直线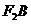 上有一点
上有一点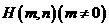 在
在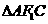 的外接圆上,求
的外接圆上,求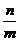 的值
的值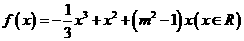 ,其中
,其中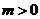
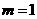 时,求曲线
时,求曲线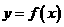 在点
在点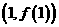 处的切线的斜率
处的切线的斜率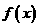 的单调区间与极值
的单调区间与极值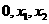 ,且
,且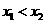 ,若对任意的
,若对任意的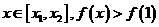 恒成立,求
恒成立,求 的取值范围
的取值范围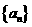 的公差不为0.设
的公差不为0.设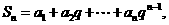
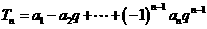
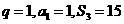 ,求数列
,求数列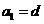 ,且
,且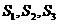 成等比数列,求
成等比数列,求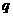 的值
的值
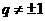 ,证明
,证明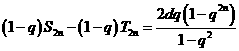
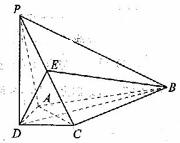 如图,在四棱锥
如图,在四棱锥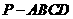 中,
中,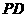
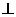 平面
平面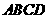 ,
,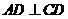 ,
,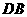 平分
平分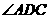 ,
,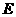 为的
为的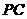 中点,
中点,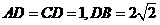
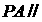 平面
平面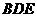
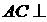 平面
平面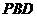
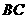 与平面
与平面