0 53377 53385 53391 53395 53401 53403 53407 53413 53415 53421 53427 53431 53433 53437 53443 53445 53451 53455 53457 53461 53463 53467 53469 53471 53472 53473 53475 53476 53477 53479 53481 53485 53487 53491 53493 53497 53503 53505 53511 53515 53517 53521 53527 53533 53535 53541 53545 53547 53553 53557 53563 53571 447348
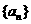 满足
满足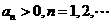 ,且
,且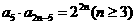 ,则当
,则当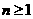 时,
时,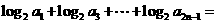
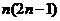 B.
B.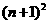 C.
C.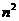 D.
D.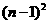
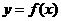 是函数
是函数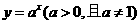 的反函数,其图像经过点
的反函数,其图像经过点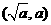 ,则
,则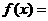
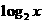 B.
B.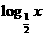 C.
C.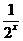 D.
D.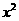
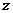 是复数,
是复数,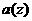 表示满足
表示满足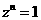 的最小正整数
的最小正整数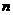 ,则对虚数单位
,则对虚数单位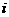 ,
,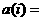
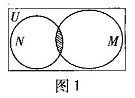 巳知全集
巳知全集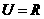 ,集合
,集合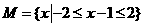 和
和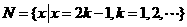 的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有
的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有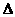 ABC中,C-A=
ABC中,C-A=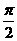 , sinB=
, sinB=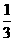 。
。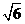 ,求
,求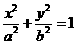 (a>b>0)的离心率为
(a>b>0)的离心率为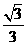 ,以原点为圆心。椭圆短半轴长半径的
,以原点为圆心。椭圆短半轴长半径的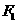 和
和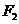 ,直线
,直线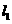 过
过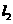 与y
与y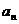 } 的前n项和
} 的前n项和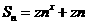 ,数列{
,数列{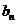 }的前n项和
}的前n项和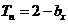
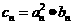 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时,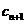 <
<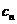
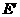 和
和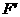 是平面ABCD内的两
是平面ABCD内的两
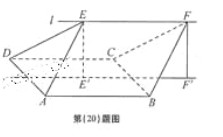
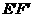 和
和 ,EF=2,求多面
,EF=2,求多面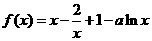 ,a>0,
,a>0,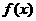 的单调性;
的单调性;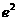 }上值域。期中e=2.71828…是自然对数的底数。
}上值域。期中e=2.71828…是自然对数的底数。
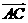 =
=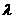
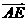 +
+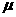
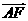 ,其中
,其中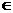 R ,则
R ,则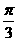 )+sin
)+sin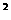 x。
x。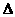
 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=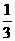 ,f(
,f(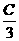 )=
)=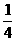 ,且C为锐角,求sinA.
,且C为锐角,求sinA.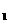 B
B
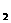 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用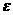 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
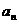 }的前n项和为
}的前n项和为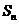 , 已知对任意的
, 已知对任意的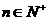 ,点
,点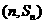 ,均在函数
,均在函数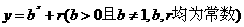 的图像上。
的图像上。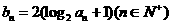
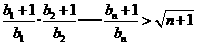 成立
成立 上选择一点C建造垃圾处理厂,其对城市的影响度
与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度
与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在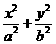 =1(a,b>0)过M(2,
=1(a,b>0)过M(2,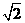 ) ,N(
) ,N(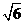 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,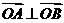 ?若存在,写出该院的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该院的方程,并求|AB |的取值范围,若不存在说明理由。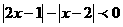 的解集为
。
的解集为
。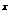 -x-a(a
-x-a(a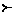 0且a
0且a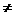 1)有两个零点,则实数a的取值范围是 。
1)有两个零点,则实数a的取值范围是 。
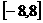 上有四个不同的根,
上有四个不同的根,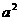 } ,若A
} ,若A 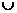 B ={ 0,
1, 2, 4 ,16},则a 的值为
B ={ 0,
1, 2, 4 ,16},则a 的值为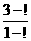 等于
等于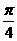 个单位,再向上平移1个单位,所得图像的函数解析式是
个单位,再向上平移1个单位,所得图像的函数解析式是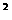 x (C)y=1+sin(2x+
x (C)y=1+sin(2x+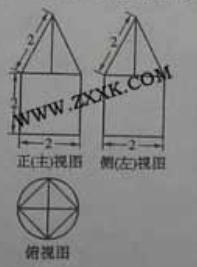
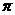 +2
+2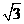 (B)4
(B)4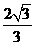 (D)2
(D)2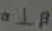 ”是“
”是“ ”的
”的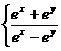 的图像大致为
的图像大致为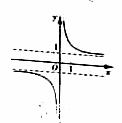
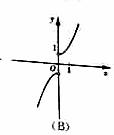
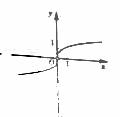
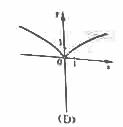
 (7)设P是 ABC所在平面内的一点,
(7)设P是 ABC所在平面内的一点,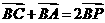 ,则
,则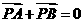 (B)
(B)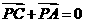
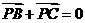 (D)
(D)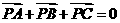
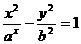 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x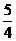 (B) 5 (C)
(B) 5 (C)
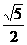 (D)
(D)
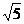
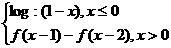 ,则f(2009)的值为:
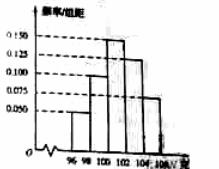
,则f(2009)的值为: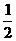 之间的概率为
之间的概率为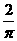 (C)
(C)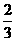
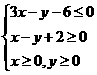 ,若目标函数z=ax+by(a>0,b>0)的是最大值为12,则其的最小值为
,若目标函数z=ax+by(a>0,b>0)的是最大值为12,则其的最小值为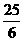 (B)
(B)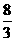 (C)
(C) 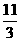 (D) 4
(D) 4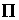 卷
卷 中,有一组对角线长为
中,有一组对角线长为 的正方形
的正方形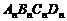
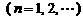 ,其对角线
,其对角线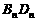 依次放置在
依次放置在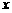 轴上(相邻顶点重合). 设
轴上(相邻顶点重合). 设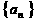 是首项为
是首项为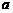 ,公差为
,公差为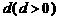 的等差数列,点
的等差数列,点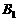 的坐标为
的坐标为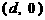 .
.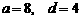 时,证明:顶点
时,证明:顶点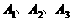 不在同一条直线上;
不在同一条直线上;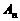 均落在抛物线
均落在抛物线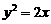 上;
上;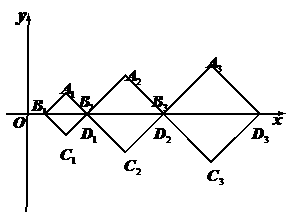 (3)为使所有顶点
(3)为使所有顶点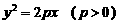 上,求
上,求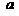 与
与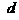 之间所应满足的关系式.
之间所应满足的关系式.