摘要:极限内容和简单的函数求导在高考中以填空题和解答题为主.考生应立足基础只是和基本方法的复习.以课本题目为主.以熟练技能.巩固概念为目标.
网址:http://m.1010jiajiao.com/timu3_id_524182[举报]
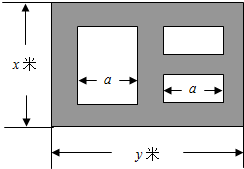 (2011•蓝山县模拟)某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(2011•蓝山县模拟)某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
下列函数求导运算正确的个数为( )
①(3x)′=3xlog3e;
②(log2x)′=
③(ex)′=ex;
④(
)′=x;
⑤(x?ex)′=ex+1.
①(3x)′=3xlog3e;
②(log2x)′=
| 1 |
| xln2 |
③(ex)′=ex;
④(
| 1 |
| lnx |
⑤(x?ex)′=ex+1.
| A、1 | B、2 | C、3 | D、4 |
考查复合函数求导的基础知识以及导数知识的综合应用.
已知函数f(x)=ln(ax+1)+
,x≥0,其中a>0.
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
查看习题详情和答案>>
已知函数f(x)=ln(ax+1)+
| 1-x | 1+x |
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
在某次试验中,有两个试验数据x,y,统计的结果如下面的表格1.
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
2 |
3 |
4 |
4 |
5 |
|


(1)在给出的坐标系中画出x,y的散点图。
(2)补全表格2,然后根据表格2的内容和公式 ,
,

1求出y对x的回归直线方程 中回归系数
中回归系数
2估计当x为10时 的值是多少?
的值是多少?
查看习题详情和答案>>


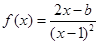 ,求导函数
,求导函数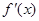 ,并确定
,并确定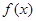 的单调区间
的单调区间