摘要:7.(北师大版第54页A组第6题)值域 变式1: 解:作出函数的图象.容易发现在上是增函数.在上是减函数.求出...注意到函数定义不包含.所以函数值域是. 变式2:解:∵ y= cos2x+sinx=-2sin2x+sinx+1.令t= sinx Î [-1,1]. 则y=-2t2+t+1.其中tÎ [-1,1]. ∴y Î [-2, ].即原函数的值域是[-2, ]. 变式3: 解:(I) ∵ f (1 + x) = f (1-x). ∴ - = 1. 又方程 f (x) = x 有等根 Û a x 2 + (b-1) x = 0 有等根. ∴ △= (b-1) 2 = 0 Þ b = 1 Þ a = -. ∴ f (x) = -x 2 + x. (II) ∵ f (x) 为开口向下的抛物线.对称轴为 x = 1. 1° 当 m≥1 时.f (x) 在 [m,n] 上是减函数. ∴ 3m = f (x)min = f (n) = -n 2 + n (*). 3n = f (x)max = f (m) = -m 2 + m. 两式相减得:3 (m-n) = -(n 2-m 2) + (n-m). ∵ 1≤m < n.上式除以 m-n 得:m + n = 8. 代入 (*) 化简得:n 2-8n + 48 = 0 无实数解. 2° 当 n≤1 时.f (x) 在 [m,n] 上是增函数. ∴ 3m = f (x)min = f (m) = -m 2 + m. 3n = f (x)max = f (n) = -n 2 + n. ∴ m = -4.n = 0. 3° 当 m≤1≤n 时.对称轴 x = 1 Î [m,n]. ∴ 3n = f (x)max = f (1) = Þ n = 与 n≥1 矛盾. 综合上述知.存在 m = -4.n = 0 满足条件.
网址:http://m.1010jiajiao.com/timu3_id_522031[举报]
已知函数f(x)为定义域为R的偶函数,当x≥0时,f(x)=log2(x+1)
(1)当x<0时,求f(x)的解析式;
(2)作出函数f(x)的图象,并指出其单调区间,以及在每一个单调区间上,它是增函数还是减函数,并指出f(x)的值域.(不要求证明)
查看习题详情和答案>>
(1)当x<0时,求f(x)的解析式;
(2)作出函数f(x)的图象,并指出其单调区间,以及在每一个单调区间上,它是增函数还是减函数,并指出f(x)的值域.(不要求证明)
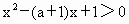 .
.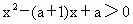
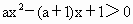 ,(a≠0)
,(a≠0)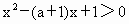 .
.
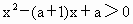
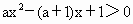 ,(a≠0)
,(a≠0)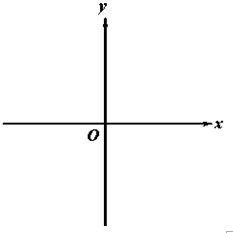 已知函数y=f(x)是定义在R上的奇函数,且当x<0时,f(x)=1+2x.
已知函数y=f(x)是定义在R上的奇函数,且当x<0时,f(x)=1+2x.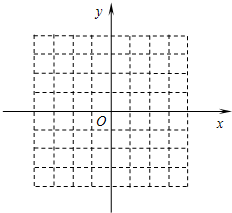 已知f(x)为R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=-1,不等式组
已知f(x)为R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=-1,不等式组