摘要:2.(人教A版选修1-1.2-1第40页练习第3题) 已知经过椭圆的右焦点作垂直于x轴的直线A B.交椭圆于A.B两点.是椭圆的左焦点. (1)求的周长, (2)如果AB不垂直于x轴.的周长有变化吗?为什么? 变式1:设椭圆的两个焦点分别为F1..F2.过F2作椭圆长轴的垂线交椭圆于点P.若△F1PF2为等腰直角三角形.则椭圆的离心率是 A. B. C. D. 解一:设椭圆方程为.依题意.显然有.则.即.即.解得.选D. 解二:∵△F1PF2为等腰直角三角形.∴. ∵.∴.∴.故选D. 变式2:已知双曲线的左.右焦点分别为.点P在双曲线的右支上.且.则此双曲线的离心率e的最大值为 . 解一:由定义知.又已知.解得..在中.由余弦定理.得.要求的最大值.即求的最小值.当时.解得.即的最大值为. 解二:设.由焦半径公式得.∵.∴.∴.∵.∴.∴的最大值为. 变式3:已知椭圆的中心为坐标原点O.焦点在轴上.斜率为1且过椭圆右焦点F的直线交椭圆于A.B两点.与共线. (Ⅰ)求椭圆的离心率, (Ⅱ)设M为椭圆上任意一点.且.证明为定值. 解:(Ⅰ)设椭圆方程为. 则直线AB的方程为.代入.化简得 . 设A().B).则 由与共线.得 又. 即.所以. 故离心率 知.所以椭圆可化为 设.由已知得 在椭圆上. 即① 由(Ⅰ)知 又.代入①得 故为定值.定值为1.
网址:http://m.1010jiajiao.com/timu3_id_519633[举报]
已知经过椭圆![]() 的右焦点F2作垂直于x轴的直线AB,交椭圆于A,B两点,F1是椭圆的左焦点.
的右焦点F2作垂直于x轴的直线AB,交椭圆于A,B两点,F1是椭圆的左焦点.
(1)求△AF1B的周长;
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?
已知经过椭圆![]() 的右焦点F2作垂直于x轴的直线AB,交椭圆于A,B两点,F1是椭圆的左焦点.
的右焦点F2作垂直于x轴的直线AB,交椭圆于A,B两点,F1是椭圆的左焦点.
(1)求△AF1B的周长;
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?
已知双曲线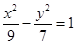 与椭圆
与椭圆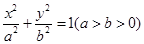 有相同的焦点,点
有相同的焦点,点 、
、 分别是椭圆的右、右顶点,若椭圆经过点
分别是椭圆的右、右顶点,若椭圆经过点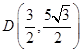 .
.
(1)求椭圆的方程;
(2)已知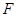 是椭圆的右焦点,以
是椭圆的右焦点,以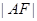 为直径的圆记为
为直径的圆记为 ,过点
,过点 引圆
引圆 的切线,求此切线的方程;
的切线,求此切线的方程;
(3)设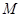 为直线
为直线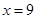 上的点,
上的点,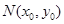 是圆
是圆 上的任意一点,是否存在定点
上的任意一点,是否存在定点 ,使得
,使得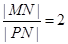 ?若存在,求出定点
?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 与椭圆
与椭圆 有相同的焦点,点
有相同的焦点,点 、
、 分别是椭圆的右、右顶点,若椭圆经过点
分别是椭圆的右、右顶点,若椭圆经过点 .
. 是椭圆的右焦点,以
是椭圆的右焦点,以 为直径的圆记为
为直径的圆记为 ,过点
,过点 引圆
引圆 为直线
为直线 上的点,
上的点, 是圆
是圆 ,使得
,使得 ?若存在,求出定点
?若存在,求出定点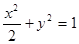 的右焦点作倾斜角为
的右焦点作倾斜角为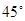 的直线
的直线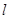 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则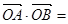 ( )
( )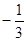 C
. -3或
C
. -3或