摘要：垂直转化 每一垂直或平行的判定就是从某一垂直或平行开始转向另一垂直或平行最终达到目的. 例如:有两个平面垂直时.一般要用性质定理.在一个平面内作交线的垂线.使之转化为线面垂直.然后进一步转化为线线垂直.
网址：http://m.1010jiajiao.com/timu3_id_510058[举报]
下列叙述中不正确的是
①若直线的斜率存在，则必有倾斜角与之对应；
②每一条直线都有唯一对应的倾斜角；
③与坐标轴垂直的直线的倾斜角为0°或90°；
④若直线的倾斜角为α，则直线的斜率为tanα．
查看习题详情和答案>>
④
④
．（填所选的序号）①若直线的斜率存在，则必有倾斜角与之对应；
②每一条直线都有唯一对应的倾斜角；
③与坐标轴垂直的直线的倾斜角为0°或90°；
④若直线的倾斜角为α，则直线的斜率为tanα．
下列叙述中不正确的是 ．（填所选的序号）
①若直线的斜率存在，则必有倾斜角与之对应；
②每一条直线都有唯一对应的倾斜角；
③与坐标轴垂直的直线的倾斜角为
或
；
④若直线的倾斜角为
，则直线的斜率为
．
定义：如果一个向量列从第二项起，每一项与它的前一项的差都等于同一个常向量，那么这个向量列叫做等差向量列，这个常向量叫做等差向量列的公差．已知向量列{
}是以
=(1，3)为首项，公差
=(1，0)的等差向量列．若向量
与非零向量
=(xn，xn+1)(n∈N*)垂直，则
=（ ）
| an |
| a1 |
| d |
| an |
| bn |
| x10 |
| x1 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
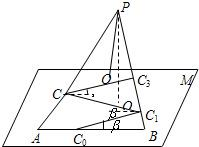某旅游景区的观景台P位于高（山顶到山脚水平面M的垂直高度PO）为2Km的山峰上，山脚下有一段位于水平线上笔直的公路AB，山坡面可近似地看作平面PAB，且△PAB为等腰三角形．山坡面与脚所在水平面M所成的二面角为α（0°＜α＜90°），且sinα=| 2 |
| 5 |
| 1 |
| 4 |
（1）试问：垂直高度每升高100米，盘山公路需修建多长？若修建盘山公路至半山腰（高度为山高的一半），在半山腰的中心Q处修建上山缆车索道站，索道PQ依山而建（与山坡面平行，离坡面高度忽略不计），问盘山公路的长度和索道的长度各是多少？
（2）若修建盘山公路为xKm，其造价为
| x2+100 |
| 2 |
问修建盘山公路至多高时，再修建上山索道至观景台，总造价最少． 查看习题详情和答案>>
在直角坐标平面上有一点列P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），…，对一切正整数n，点Pn在函数y=3x+
的图象上，且Pn的横坐标构成以-
为首项，-1为公差的等差数列{xn}．
（1）求点Pn的坐标；
（2）设抛物线列C1，C2，C3，…，Cn，…中的每一条的对称轴都垂直于x轴，抛物线Cn的顶点为Pn，且过点Dn（0，n2+1）．记与抛物线Cn相切于点Dn的直线的斜率为kn，求
+
+…+
；
（3）设S={x|x=2xn，n∈N*}，T={y|y=4yn，n∈N*}，等差数列{an}的任一项an∈S∩T，其中a1是S∩T中的最大数，-265＜a10＜-125，求数列{an}的通项公式． 查看习题详情和答案>>
| 13 |
| 4 |
| 5 |
| 2 |
（1）求点Pn的坐标；
（2）设抛物线列C1，C2，C3，…，Cn，…中的每一条的对称轴都垂直于x轴，抛物线Cn的顶点为Pn，且过点Dn（0，n2+1）．记与抛物线Cn相切于点Dn的直线的斜率为kn，求
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
（3）设S={x|x=2xn，n∈N*}，T={y|y=4yn，n∈N*}，等差数列{an}的任一项an∈S∩T，其中a1是S∩T中的最大数，-265＜a10＜-125，求数列{an}的通项公式． 查看习题详情和答案>>