0 50759 50767 50773 50777 50783 50785 50789 50795 50797 50803 50809 50813 50815 50819 50825 50827 50833 50837 50839 50843 50845 50849 50851 50853 50854 50855 50857 50858 50859 50861 50863 50867 50869 50873 50875 50879 50885 50887 50893 50897 50899 50903 50909 50915 50917 50923 50927 50929 50935 50939 50945 50953 447348
 充分但不必要条件
B
充分但不必要条件
B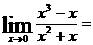
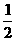 C
C 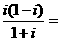
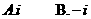 C
1
D -1
C
1
D -1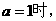
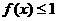
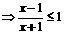 ,化为
,化为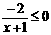 ……(3分)
……(3分)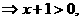
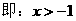
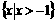
 ……(5分)
……(5分)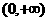 上任取
上任取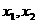 ,则
,则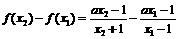 ……(7分)
……(7分)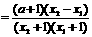 ……(8分)
……(8分)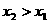 故
故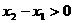 ,又在
,又在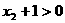 ,
,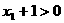 ……(10分)
……(10分)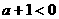 时,即
时,即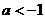 时
时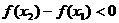 , ……(12分)
, ……(12分)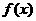 在
在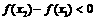 求出
求出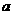 的充分性扣2分
的充分性扣2分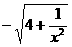 ,数列{
,数列{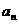 }的前n项和记为
}的前n项和记为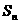 ,点
,点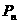 (
(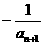 )在曲线y=f(x)上(n∈N+),且
)在曲线y=f(x)上(n∈N+),且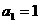 ,
, 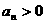
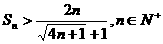
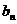 }的前n项和为
}的前n项和为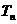 ,且满足:
,且满足: 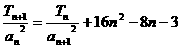
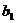 的值,使得数列{
的值,使得数列{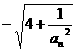 , 并且
, 并且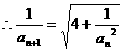 ,
, 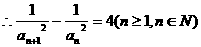
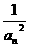 }为等差数列,并且首项为
}为等差数列,并且首项为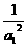 =1,公差为4 ……(4分)
=1,公差为4 ……(4分)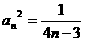
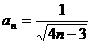 ……(5分)
……(5分)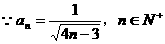
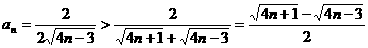 ……(8分)
……(8分)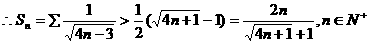 ……(10分)
……(10分)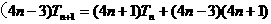
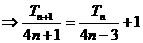 ……(12分)
……(12分)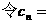
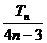 ,如果
,如果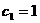 ,此时
,此时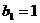
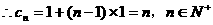 ……(13分)
……(13分)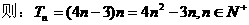
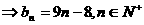 ,
,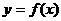 对于区间D上的任意两个值
对于区间D上的任意两个值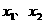 总有以下不等式
总有以下不等式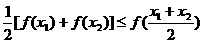 成立,则称函数
成立,则称函数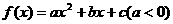 是凸函数;
是凸函数;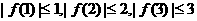 ,求
,求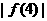 取得最大值时函数
取得最大值时函数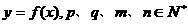 ,
,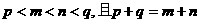 ,证明:
,证明: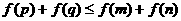
 R,则
R,则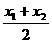 )-[f(x1)+f(x2)]
)-[f(x1)+f(x2)]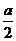 [(x1+x2)2-2(x12+x22)]=
-
[(x1+x2)2-2(x12+x22)]=
- a<0
a<0
 2f(
2f( 0
0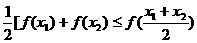
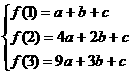 解得
解得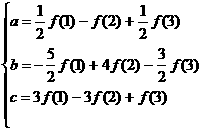 ……(5分)
……(5分) |f(1)|+3|f(2)|+3|f(3)|
|f(1)|+3|f(2)|+3|f(3)| 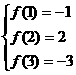 时取等号,代入上式得
时取等号,代入上式得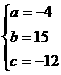
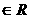 且p<m<n<q
且p<m<n<q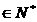
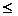 f(p+i)+f(p+k-i)
f(p+i)+f(p+k-i)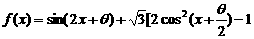 ] ………………2分
] ………………2分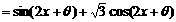 ……(4分)
……(4分)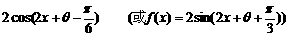 ……………6分
……………6分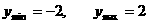 ………………8分
………………8分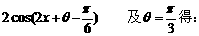
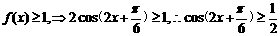 ……………………12分
……………………12分 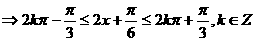
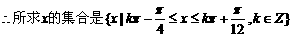 …………14分
…………14分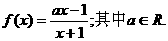
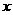 的集合;
的集合;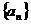 满足:
满足: 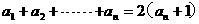 ,
,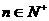
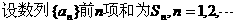 依题意得:
依题意得: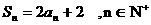 …………2分
…………2分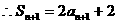
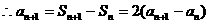 (n=1,2,…)…………5分
(n=1,2,…)…………5分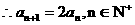 …………8分
…………8分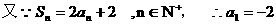
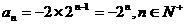 …………12分
…………12分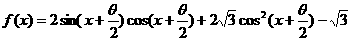
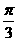 时,求函数
时,求函数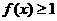 的x的集合
的x的集合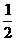 , sinC=
, sinC=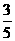 ,
, 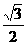 , 又sinC=
, 又sinC=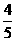 , …………4分
, …………4分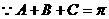
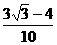 , …………12分
, …………12分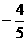 ,扣3分)
,扣3分)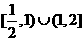
 ②③或 ①③
②③或 ①③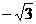 12
12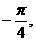
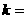 1
1