摘要:18.解:(Ⅰ)当,化为-- 故.满足(Ⅰ)条件的集合为 -- (Ⅱ)在区间上任取.则-- -- 因故.又在上, -- ∴只有当时.即时 才总有, -- ∴当时,在上是单调减函数 说明:本题若令求出.没有考虑的充分性扣2分 19 已知:f(x)=,数列{}的前n项和记为,点(,)在曲线y=f(x)上(n∈N+).且. (I)求数列{}的通项公式; (II)求证: (Ⅲ)数列{}的前n项和为.且满足: 设定的值.使得数列{}是等差数列 19 解:(Ⅰ)由于y= ∵点An(,)在曲线y=f(x)上(n∈N+) ∴= f()= , 并且 -- . ∴数列{}为等差数列.并且首项为=1.公差为4 -- ∴=1+4(n-1) . ∴ ∵ . ∴ -- (II) -- -- (Ⅲ)由 . 得: -- .如果.此时 -- . 此时.数列{}是等差数列 -- 20 若定义在区间D上的函数对于区间D上的任意两个值总有以下不等式成立.则称函数为区间D上的凸函数 , (1)证明:定义在R上的二次函数是凸函数, 中的二次函数. 若,求取得最大值时函数的解析式, (3)定义在R上的任意凸函数, 若.证明: 20 证明:(1)任取x1 x2R,则 2f()-[f(x1)+f(x2)] =2[a()2 + b+c] -[a x12+bx1+c] - [a x22+bx2+c] =[(x1+x2)2-2(x12+x22)]= -(x1-x2)2 -- a<0 2f()-[f(x1)+f(x2)] 0 由定义得 y = f(x)是R上的凸函数 -- (2)解得 -- |f-3f||f| |f(1)| 1.|f(2)| 2,|f(3)| 3 |f(4)| |f| 16 -- a<0时f(x)= ax2+bx+c开口向下. 当且仅当时取等号.代入上式得 f(x)= -4x2+15x-12 -- (3) p q m n且p<m<n<q 不妨设m = p+i, 其中i p+q = m+n m-p = q-n = i 由定义知.任意x1 x2R,有f(x1)+f(x2) 2f() -- 取x1 = p x2 = p+2则有f 2f(p+1) 变形得f f 同理有 f f f f f f - - f f 累加求和得:f f 即 f f -- 递推i次得 f f f - f f f 令p+k = q,得f f m-p = q-n = i f f --
网址:http://m.1010jiajiao.com/timu3_id_508567[举报]
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
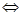
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
查看习题详情和答案>>
(2013•崇明县二模)已知函数f(x)=sinx+acos2
(a为常数,a∈R),且x=
是方程f(x)=0的解.当x∈[0,π]时,函数f(x)值域为
查看习题详情和答案>>
| x |
| 2 |
| π |
| 2 |
[-2,
-1]
| 2 |
[-2,
-1]
.| 2 |
已知直线y=k(x-2)(k∈R)与双曲线
-
=1,某学生作了如下变形;由
消去y后得到形如关于x的方程ax2+bx+c=0.讨论:当a=0时,该方程恒有一解;当a≠0时,b2>4ac恒成立,假设该学生的演算过程是正确的,则根据该学生的演算过程所提供的信息,求出实数m的取值范围应为( )
| x2 |
| m |
| y2 |
| 8 |
|
查看习题详情和答案>>
已知函数 ,
, .
.
(Ⅰ)若函数 和函数
和函数 在区间
在区间 上均为增函数,求实数
上均为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有唯一解,求实数
有唯一解,求实数 的值.
的值.
【解析】第一问, 
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数
上均为增函数
(Ⅱ)中方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解得到结论。
有唯一解得到结论。
(Ⅰ)解:
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数 ……………6分
上均为增函数 ……………6分
(Ⅱ)方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解
有唯一解
查看习题详情和答案>>






