5.计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符
号,这些符号与十进制的数的对应关系如下表:
|
十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
例如:用十六进制表示:E+D=1B,则A×B=
A.6E B.72 C.5F D.B0
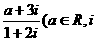 为虚数单位)是纯虚数,则实数a的值为 ( )
为虚数单位)是纯虚数,则实数a的值为 ( )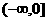 上是减函数,且f(2)=0,则使得f(x)<0的x
上是减函数,且f(2)=0,则使得f(x)<0的x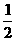 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )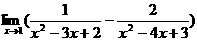 = ( )
= ( )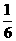 D.
D.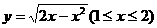 反函数是 ( )
反函数是 ( )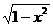 (-1≤x≤1) B.y=1+
(-1≤x≤1) B.y=1+ 已
已 (C1S2∩C1S3)
(C1S2∩C1S3)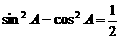 ,得
,得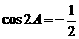 .
.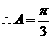 . …………………………..3分
. …………………………..3分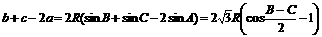 ………..9分
………..9分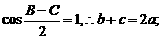
 若B¹C,则
若B¹C,则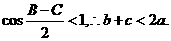 ………………………..12分
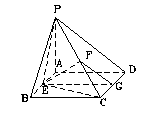
………………………..12分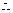 AD是PD在平面ABCD内的射影。
AD是PD在平面ABCD内的射影。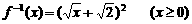 .…………………………..4分
.…………………………..4分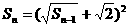

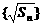 是首项为
是首项为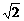 、公差为
、公差为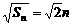 ,由
,由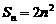 ,可求得
,可求得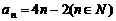 .…8分
.…8分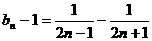 ,
,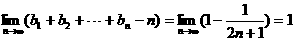 .………….12分
.………….12分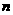 年该公司共有
年该公司共有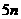 名职工,基础工资总额为
名职工,基础工资总额为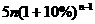 万元,
万元, 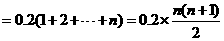
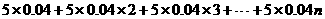
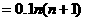 万元, ……….……………………..4分
万元, ……….……………………..4分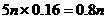 (万元)
(万元) 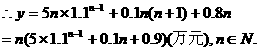 …………6分
…………6分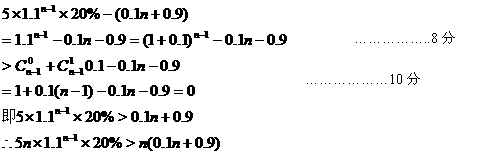 (II)
(II)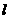 为
为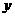 轴,且点
轴,且点 在
在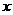 轴的正半轴上建立直角坐标系,则
轴的正半轴上建立直角坐标系,则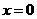 ,
,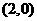 ,设点
,设点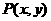 是曲线段
是曲线段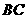 上任意一点,则
上任意一点,则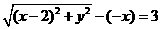 ,
,
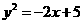
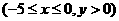 .………..4分
.………..4分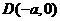
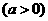 ,点
,点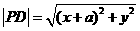
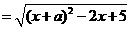
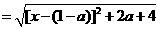 ,…….6分
,…….6分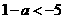 即
即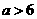 ,则当
,则当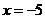 时,
时,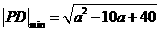 ;………..8分
;………..8分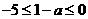 即
即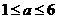 ,则当
,则当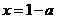 时,
时,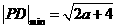 ;……….10分
;……….10分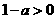 即
即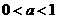 ,则当
,则当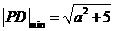 .………..12分
.………..12分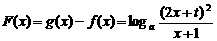 ,
……….……2分
,
……….……2分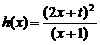 ,
,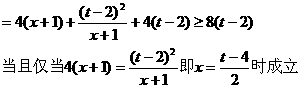
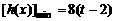 . ……………….………..6分
. ……………….………..6分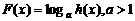 ,
,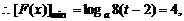 从而
从而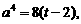
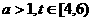 ,
,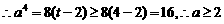 ,等号在t=4, x=0时取得.….……….8分
,等号在t=4, x=0时取得.….……….8分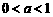 时,
时,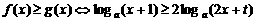
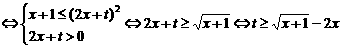 .
.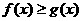 恒成立,只要
恒成立,只要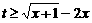 恒成立,
恒成立,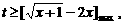 …………………11分
…………………11分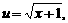 则
则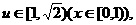
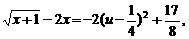 当u=1时,
当u=1时,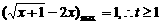 ,
,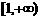 .…………………………..………….14分
.…………………………..………….14分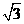 (14)
(14)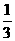 或-2
(15)
或-2
(15)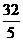 (16)540
(16)540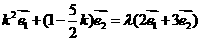 ,得
,得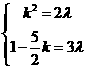 ,可解.
,可解.