25.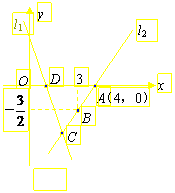 如图,直线
如图,直线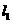 的函数表达式为
的函数表达式为 ,且
,且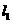 与
与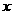 轴交于点
轴交于点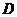 ,直线
,直线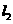 经过点
经过点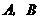 ,直线
,直线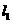 ,
,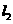 交于点
交于点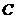 .
.
(1)求点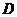 的坐标;
的坐标;
(2)求直线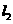 的函数表达式;
的函数表达式;
(3)求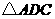 的面积;
的面积;
(4)在直线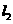 上存在异于点
上存在异于点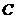 的另一点
的另一点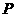 ,使得
,使得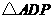
|
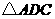 的面积相等,请直接写出点
的面积相等,请直接写出点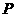 的坐标.
的坐标.
25. 如图,直线
如图,直线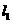 的函数表达式为
的函数表达式为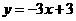 ,且
,且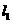 与
与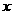 轴交于点
轴交于点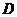 ,直线
,直线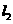 经过点
经过点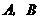 ,直线
,直线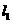 ,
,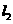 交于点
交于点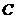 .
.
(1)求点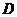 的坐标;
的坐标;
(2)求直线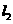 的函数表达式;
的函数表达式;
(3)求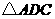 的面积;
的面积;
(4)在直线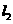 上存在异于点
上存在异于点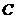 的另一点
的另一点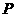 ,使得
,使得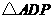
|
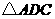 的面积相等,请直接写出点
的面积相等,请直接写出点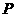 的坐标.
的坐标.