0 445179 445187 445193 445197 445203 445205 445209 445215 445217 445223 445229 445233 445235 445239 445245 445247 445253 445257 445259 445263 445265 445269 445271 445273 445274 445275 445277 445278 445279 445281 445283 445287 445289 445293 445295 445299 445305 445307 445313 445317 445319 445323 445329 445335 445337 445343 445347 445349 445355 445359 445365 445373 447348
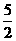 )x<(k2-2k+
)x<(k2-2k+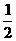 (B)x<
(B)x<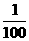 ,1)
(B)(100,+∞)
,1)
(B)(100,+∞) ,E是A1C的中点,
,E是A1C的中点,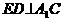 且交AC于D,
且交AC于D,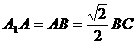 。
。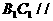 平面
平面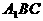 ;
;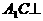 平面
平面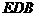 ;
;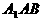 与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。
与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。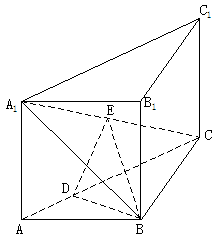
 三棱柱
三棱柱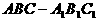 中
中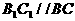 , 1分
, 1分 平面
平面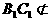 平面
平面 平面
平面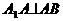 ,
, 中
中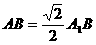
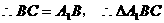 是等腰三角形 6分
是等腰三角形 6分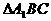 底边
底边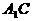 的中点,
的中点,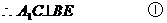
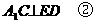
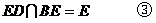
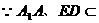 平面
平面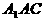 ,
,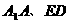 不平行,
不平行,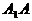 ,ED后必相交,
,ED后必相交,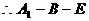 是所求的二面角 10分
是所求的二面角 10分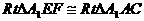
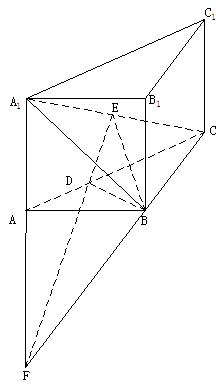
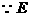 为
为 A为
A为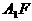 中点
中点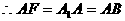
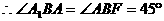
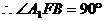
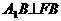 12分
12分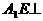 平面EFB,
平面EFB,
 是所求的二面角的平面角 13分
是所求的二面角的平面角 13分
 14分
14分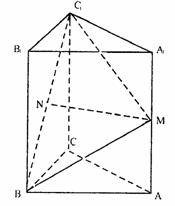 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2 ,∠ACB=90°,M是AA1的中点,N是BC1中点.
,∠ACB=90°,M是AA1的中点,N是BC1中点.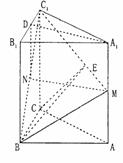 又,
又,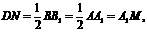 所以四边形A1MND为平行四边形,
所以四边形A1MND为平行四边形,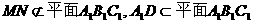 ,
,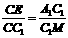
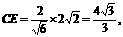 ……………………11分
……………………11分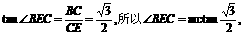 ……………………13分
……………………13分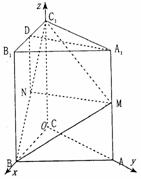 即二面角B-C1M-A的大小为
即二面角B-C1M-A的大小为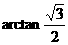 .…………………14分
.…………………14分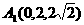 、
、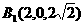 、
、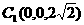 .
.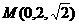 ,
,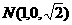 ,
,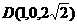
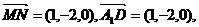
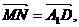 …………2分
所以MN//A1N;………………4分
…………2分
所以MN//A1N;………………4分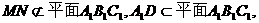 所以MN//平面A1B1C1;…………5分
所以MN//平面A1B1C1;…………5分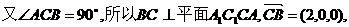 ………………7分
………………7分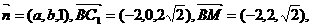
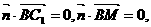 即
即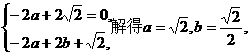
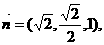 ……………………………………10分
……………………………………10分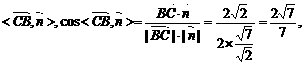 ……………13分
……………13分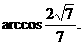 …………………………14分
…………………………14分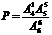 ……………………5分
……………………5分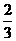 ;……………………6分
;……………………6分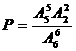 ……………………11分
……………………11分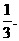 …………………………12分
…………………………12分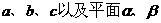 ,给出下列命题:
,给出下列命题: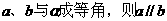 ②若
②若
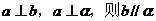 ④若
④若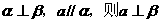
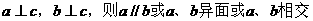
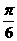 ___,球的表面积为__
___,球的表面积为__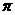 ________(不计损耗)。
________(不计损耗)。