摘要:18. 如图.在直三棱柱ABC-A1B1C1中.AC=BC=2.AA1=2.∠ACB=90°.M是AA1的中点.N是BC1中点. (Ⅰ)求证:MN∥平面A1B1C1, (Ⅱ)求二面角B-C1M-A的大小. 解:方法一(Ⅰ)取B1C1中点D.连结ND.A1D. 所以DN//BB1///AA1.------1分 又.所以四边形A1MND为平行四边形. 所以MN//A1D,----3分 又. 所以MN//平面A1B1C1,----5分 (Ⅱ)三棱柱ABC-A1B1C1为直三棱柱.所以CC1⊥BC. 又∠ACB=90°.所以BC⊥平面ACC1A1.----7分 在平面ACC1A1上作CE⊥C1M.交C1M于点E. 则CE为BE在平面ACC1A1上的射影. 所以∠BEC为二面角B-C1M-A的平面角.------9分 由于△CEC1与三角形C1A1M相似.所以 所以--------11分 所以--------13分 即二面角B-C1M-A的大小为.-------14分 方法二(Ⅰ)如图.以点C为坐标原点.以CB所在 直线为Ox轴.CA所在直线为Oy轴.CC1所在直线 为Oz轴.建立空间直角坐标系. 由已知得... ,, 所以 所以----2分 所以MN//A1N,------4分 又所以MN//平面A1B1C1,----5分 (Ⅱ)三棱柱ABC-A1B1C1为直三棱柱.所以CC1⊥BC. ------7分 设垂直于平面BMC1的向量 所以 即 所以--------------10分 所求二面角的大小-----13分 即二面角B-C1M-A的大小为----------14分
网址:http://m.1010jiajiao.com/timu3_id_4452766[举报]
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2| 2 |
(1)求证:A1B⊥平面CDE;
(2)求三棱锥A1-CDE的体积. 查看习题详情和答案>>
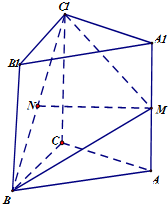 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2| 2 |
(1)求证:MN∥平面A1B1C1;
(2)求二面角B-C1M-C的平面角余弦值的大小.
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2| 2 |
(1)求证:平面CDE⊥平面ABB1A1;
(2)求二面角D-CE-A1的大小.
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=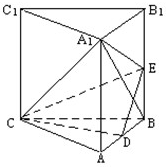 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1= ,点D是AB的中点,点E是BB1的中点.
,点D是AB的中点,点E是BB1的中点.