0 445168 445176 445182 445186 445192 445194 445198 445204 445206 445212 445218 445222 445224 445228 445234 445236 445242 445246 445248 445252 445254 445258 445260 445262 445263 445264 445266 445267 445268 445270 445272 445276 445278 445282 445284 445288 445294 445296 445302 445306 445308 445312 445318 445324 445326 445332 445336 445338 445344 445348 445354 445362 447348
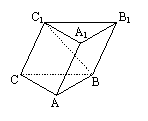 如图,在斜三棱柱A1B1C1-ABC中,∠BAC=900,BC1⊥AC,则C1在底面ABC上的射影H必在
如图,在斜三棱柱A1B1C1-ABC中,∠BAC=900,BC1⊥AC,则C1在底面ABC上的射影H必在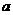 ,从一个顶点出发的三条棱两两都成600角,则该平行六面体的体积为
,从一个顶点出发的三条棱两两都成600角,则该平行六面体的体积为
 B、
B、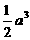 C、
C、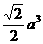 D、
D、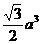
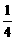 B、
B、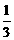 C、
C、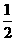 D、
D、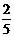
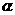 所成角为
所成角为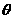 ,在
,在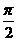 ,最小值
,最小值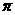 ,最小值
,最小值
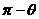 ,最小值
,最小值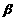 的大小为
的大小为 、
、 ,
, C、
C、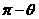 D、
D、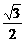 B、
B、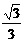 C、
C、 D、
D、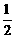
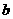 、
、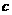 表示两条直线,
表示两条直线,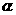 、
、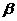 表示两个平面,下列命题中真命题是
表示两个平面,下列命题中真命题是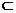
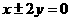 且截直线
且截直线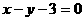 所得弦长为
所得弦长为 的双曲线方程。
的双曲线方程。 ,
,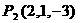 ,
,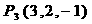 ,设
,设 ,
,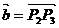
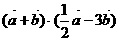 ;(2)求实数
;(2)求实数 ,使
,使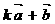 与
与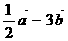 互相垂直.
互相垂直. 21(12分).如图,正三棱柱ABC-A1B1C1中,AB=4,BB1=6, D为AB的中点,
F为A1C1中点,E在BB1上,
21(12分).如图,正三棱柱ABC-A1B1C1中,AB=4,BB1=6, D为AB的中点,
F为A1C1中点,E在BB1上,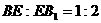 时,求异面直线CE与DF所成角的余弦
时,求异面直线CE与DF所成角的余弦 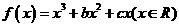 ,已知
,已知 是奇函数。
是奇函数。 、
、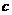 的值。
的值。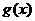 的单调区间与极值。
的单调区间与极值。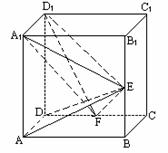 23(12分).如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
23(12分).如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.  在
在 与
与 时,都取得极值.
时,都取得极值.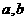 的值;(2)若
的值;(2)若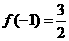 ,求
,求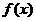 的单调区间和极值;
的单调区间和极值;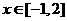 都有
都有 恒成立,求
恒成立,求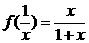 ,则
,则 _______.
_______.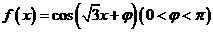 。若
。若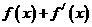 是奇函数,则
是奇函数,则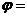 _______
_______