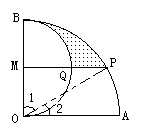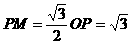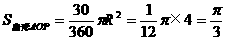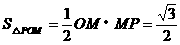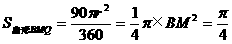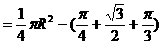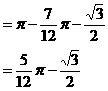0 44277 44285 44291 44295 44301 44303 44307 44313 44315 44321 44327 44331 44333 44337 44343 44345 44351 44355 44357 44361 44363 44367 44369 44371 44372 44373 44375 44376 44377 44379 44381 44385 44387 44391 44393 44397 44403 44405 44411 44415 44417 44421 44427 44433 44435 44441 44445 44447 44453 44457 44463 44471 447348
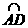 的长为___________厘米。
的长为___________厘米。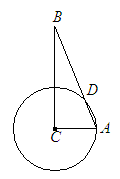
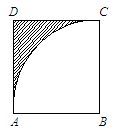
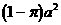 B.
B.
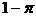
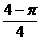 D.
D.

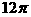 B.
B. 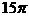 C.
C.
 D.
D. 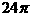
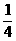 ,那么这个圆柱的侧面积是( )
,那么这个圆柱的侧面积是( ) B.
B.
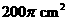
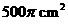 D.
D.
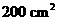
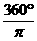 ,则扇形的面积为( )
,则扇形的面积为( )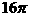
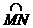 的长为( )
的长为( )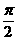 B.
B.
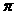 C.
C.
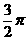 D.
D.
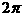
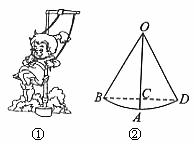
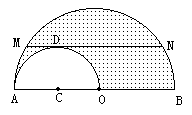
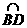 为摆动的路程。
为摆动的路程。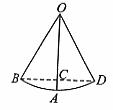
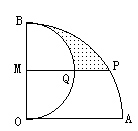
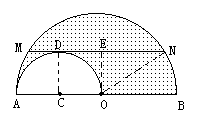
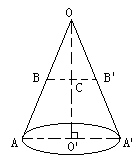
 ,∠BOD=60°
,∠BOD=60°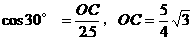
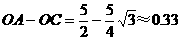 米
米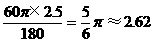 米
米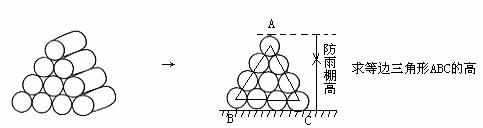
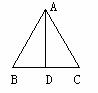
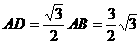 米
米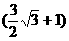 米。
米。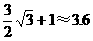 米。
米。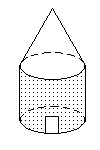
 B.
B.
 C.
C.  D.
D.
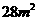
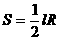
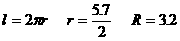
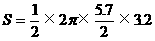
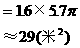
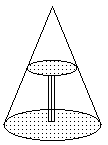
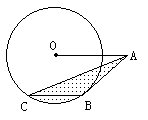
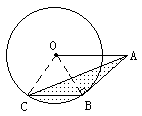
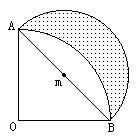
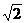 米的圆形铁皮,要从中剪出圆心角是90°的一个最大扇形ABC,求(1)被剪掉阴影部分的面积。(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)。(3)求圆锥的全面积。
米的圆形铁皮,要从中剪出圆心角是90°的一个最大扇形ABC,求(1)被剪掉阴影部分的面积。(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)。(3)求圆锥的全面积。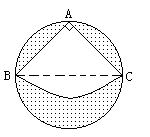
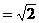
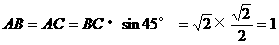
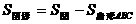
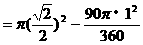
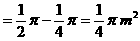
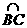 长为
长为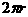
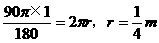
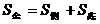
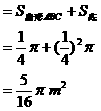
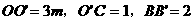
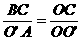
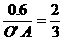
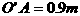
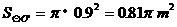
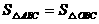
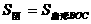
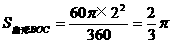
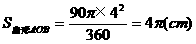
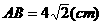
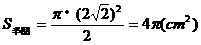
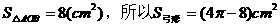
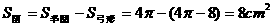
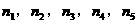
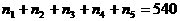
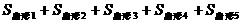
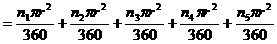
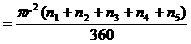
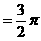
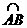 于P,求
于P,求