摘要:例1. 一个小孩荡秋千.如图所示.秋千的链子的长为OA=2.5m.当秋千向两边摆动时.摆角∠BOD恰好为60°.并且两边摆动角度相同. 求:(1)秋千摆至最高位置时与其摆至最低位置时的高度之差. (2)秋千从B点摆动到D点所走过的路程 分析:抽象出几何图形 OB=OD=OA为秋千的链子长 OA为秋千摆至最低位置 OB与OD为秋千摆至最高位置 AC为这两个位置的差 为摆动的路程. 解:连接BD交OA与C.则OA⊥BD于C .∠BOD=60° 则∠BOC=∠COD=30° Rt△OCD中. 米 (2)的长l=米 答:略. 例2. 某燃料公司的院内堆放10个外径为1米的空油桶.为了防雨.防雷.需搭建简易防雨棚.这个防雨棚的高度最低应为多少米? 分析:实际问题抽象成几何模形.用几何图形解决. 解:△ABC为等边三角形 AB=6个半径=3米 米 则防雨棚高度等于米. 答:高至少为米. 例3. 新疆哈萨克民族是一个游牧民族.喜爱居住毡房.毡房的顶部是圆锥形.如图所示.为防雨需要在毡房顶部铺上防雨布.已知圆锥的底面直径是5.7m.母线长是3.2m.铺满毡房顶部至少需要防雨布(精确到1m2)( ) A. B. C. D. 分析:求圆锥侧面积 解:∵ 选B. 例4. 如图.有一直径是米的圆形铁皮.要从中剪出圆心角是90°的一个最大扇形ABC.求(1)被剪掉阴影部分的面积.(2)用所留的扇形铁皮围成一个圆锥.该圆锥的底面圆的半径是多少?求圆锥的全面积. 分析:阴影部分面积是圆的面积减去一个圆心角为90°的扇形面积.其关键是要求出扇形的半径.由弧长等于底面周长可求出半径. 解:(1)连接BC 因为∠A=90°.所以BC为⊙O的直径.BC 在Rt△ABC中. 又 (2)设圆锥底面半径为r.则长为 所以 (3) 例5. 如图.这是圆桌上方的灯泡发出的光线.照射桌面后.在地面上形成阴影的示意图.已知桌面的直径为1.2m.桌面距离地面1m.若灯泡距离地面3m.则地面上阴影部分的面积是多少? 分析:灯泡的光线射在地面上.形成的阴影可体会成一个圆锥.要求阴影的面积.即求底面圆的半径即可. 解:由已知可作轴截面 其中 从而OC=2m.BC=0.6 由BC∥OA得: 所以 [模拟试题]
网址:http://m.1010jiajiao.com/timu3_id_443743[举报]
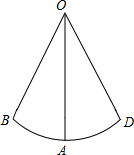
一个小孩荡秋千,如图所示,秋千链子的长OA为2.5米,当秋千向两边摆动时,摆角∠BOD恰好是60°,并且两边摆动角度相同,
求:(1)秋千摆至最高位置时与最低位置时的高度之差;
(2)秋千从B点摆动至D点所走过的路程.(结果都精确到0.01)

 查看习题详情和答案>>
查看习题详情和答案>>
求:(1)秋千摆至最高位置时与最低位置时的高度之差;
(2)秋千从B点摆动至D点所走过的路程.(结果都精确到0.01)

 查看习题详情和答案>>
查看习题详情和答案>>
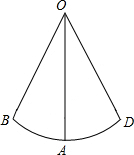
一个小孩荡秋千,如图所示,秋千链子的长OA为2.5米,当秋千向两边摆动时,摆角∠BOD恰好是60°,并且两边摆动角度相同,
求:(1)秋千摆至最高位置时与最低位置时的高度之差;
(2)秋千从B点摆动至D点所走过的路程.(结果都精确到0.01)

查看习题详情和答案>>
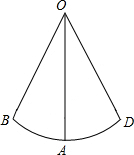
一个小孩荡秋千,如图所示,秋千链子的长OA为2.5米,当秋千向两边摆动时,摆角∠BOD恰好是60°,并且两边摆动角度相同,
求:(1)秋千摆至最高位置时与最低位置时的高度之差;
(2)秋千从B点摆动至D点所走过的路程.(结果都精确到0.01)

查看习题详情和答案>>
求:(1)秋千摆至最高位置时与最低位置时的高度之差;
(2)秋千从B点摆动至D点所走过的路程.(结果都精确到0.01)



