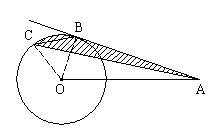
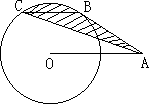
摘要:例1. 如图.A是半径为2的⊙O外一点.OA=4.AB是⊙O的切线.点B是切点.弦BC∥OA.连结AC.求图中阴影部分的面积. 分析:图中阴影部分可看作弓形BC面积与三角形ABC面积的和.而△ABC不是Rt△.所以考虑借助OA∥BC将△ABC移形.连接OC.OB.则S△OCB=S△ACB. 则阴影部分面积为扇形AOB面积. 解:连接OB.OC.因为BC∥OA 所以△ABC与△OBC在BC上的高相等 所以 所以 又∵AB是⊙O的切线 所以OB⊥AB.而OB=2.OA=4 所以∠AOB=60°. 由BC∥OA得∠OBC=60° 所以△OBC为等边三角形.∠BOC=60° 例2. 如图.扇形AOB的圆心角为直角.若OA=4.以AB为直径作半圆.求阴影部分的面积. 分析:图中阴影部分面积为: 以AB为直径的半圆面积减去弓形AmB面积, 而弓形面积等于扇形AOB面积减去△AOB面积. 解:∵OA=4cm.∠O=90°.OB=4cm ∴ 又 所以 而 故 例3. 如图.⊙A.⊙B.⊙C.⊙D.⊙E相外离.它们的半径都是1.顺次连接五个圆心得到五边形ABCDE.则图中五个扇形的面积之和是多少? 分析:五个扇形的圆心角分别为 而 解:设这个五个扇形的圆心角的度数分别为 ∵五边形ABCDE内和角等于540° 则 五个扇形面积之和等于 例4. 已知直角扇形AOB.半径OA=2cm.以OB为直径在扇形内作半圆⊙M.过M引MP∥AO交于P.求与半圆弧及MP围成的阴影部分的面积S阴. 分析:此阴影部分不是一个规则图形.不能用公式直接求解.所以考虑将它分割为可求图形的面积求解. 解:连接OP ∵OA⊥OB.又∵MP∥OA ∴MP⊥OB.又∵OM=BM=1 OP=OA=2 ∴∠1=60°.∠2=30° ∴ ∴ 设PM与半圆⊙M交于Q ∴ ∴ 例5. 如图.在两个半圆中.大圆的弦MN与小圆相切于点D.MN∥AB.MN=8cm.ON.CD分别是两圆的半径.求阴影部分的面积. 分析: 所以关键是求⊙O半径OB或OM或ON ⊙C半径AC或CO或CD 而MN为⊙C切线.CD⊥MN且CD为⊙C半径 解:过O作OE⊥MN于E.则OE平分MN ∵MN∥AB可得四边形EOCD为矩形 所以OE=CD.连接ON 在Rt△EON中 ON=4
网址:http://m.1010jiajiao.com/timu3_id_443742[举报]
(1)如图,OA、OB是⊙O的半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交DC于点E.则CD=C![]() E吗?如成立,试说明理由.
E吗?如成立,试说明理由.
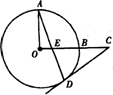
(2)若将图中的半径OB所在直线向上平行移动交OA于F,交⊙O于B’,其他条件不变,如图,那么上述结论CD=CE还成立吗?为什么?
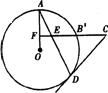
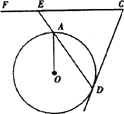
(3)若将图中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变,如图,那么上述结论CD=CE还成立吗?为什么.