0 144760 144768 144774 144778 144784 144786 144790 144796 144798 144804 144810 144814 144816 144820 144826 144828 144834 144838 144840 144844 144846 144850 144852 144854 144855 144856 144858 144859 144860 144862 144864 144868 144870 144874 144876 144880 144886 144888 144894 144898 144900 144904 144910 144916 144918 144924 144928 144930 144936 144940 144946 144954 447348
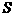 ,滑动变阻器取四个不同阻值时,可以得出电流表和电压表的四组对应的值。这四组对应的值在图乙的
,滑动变阻器取四个不同阻值时,可以得出电流表和电压表的四组对应的值。这四组对应的值在图乙的 坐标中分别用
坐标中分别用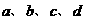 四个点表示(坐标原点表示的电压值和电流值均为零)。由这四个点作出的
四个点表示(坐标原点表示的电压值和电流值均为零)。由这四个点作出的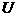 轴)于
轴)于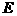 点,交横轴(
点,交横轴( 轴)于
轴)于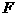 点,若电源电压为
点,若电源电压为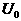 ,定值电阻的阻值为
,定值电阻的阻值为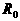 。据此分析:(1)
。据此分析:(1)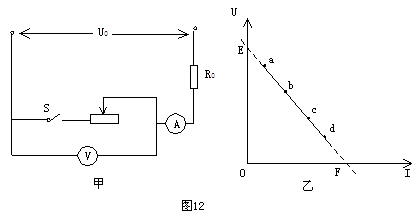
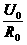 (2分)。此时S闭合且滑动变阻器的滑片P滑到了最左端,使滑动变阻器处于局部短路状态(1分)。
(2分)。此时S闭合且滑动变阻器的滑片P滑到了最左端,使滑动变阻器处于局部短路状态(1分)。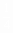 。
求:(1)当n为小于5的正整数时,求n的取值;
(2)R1、R2与n的对应值。
(01年重庆联招题)
解:(1)设电源电压为U,由RL=
。
求:(1)当n为小于5的正整数时,求n的取值;
(2)R1、R2与n的对应值。
(01年重庆联招题)
解:(1)设电源电压为U,由RL=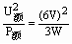 =12Ω。
当S接a时,I1=
=12Ω。
当S接a时,I1=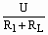 ,则灯的功率为PL=I
,则灯的功率为PL=I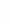 RL=
RL=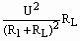 ①
当S接b时,I2=
①
当S接b时,I2=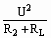 ,则灯的功率为P′L=I
,则灯的功率为P′L=I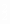 RL=
RL=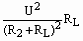 ②
又P′L=
②
又P′L=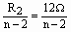 。
又R1>0、n-2>0、n>2,∴2<n<5,n的取值为3、4。
②当n=3时,R1=
。
又R1>0、n-2>0、n>2,∴2<n<5,n的取值为3、4。
②当n=3时,R1=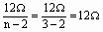 ,R2=nR1=3×12Ω=36Ω。
当n=4时,R1=
,R2=nR1=3×12Ω=36Ω。
当n=4时,R1=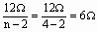 ,R2=nR1=4×6Ω=24Ω。
,R2=nR1=4×6Ω=24Ω。
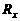 ,电阻消耗的功率为
,电阻消耗的功率为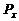 ,灯丝电阻
,灯丝电阻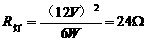
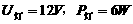
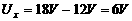
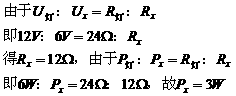

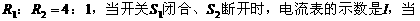
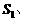
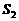 均闭合时,电流表的示数是
均闭合时,电流表的示数是 ,则
,则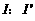 =( )
=( )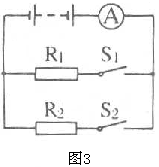
 断开时,电流表的示数就是通过
断开时,电流表的示数就是通过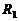 中的电流,即
中的电流,即
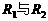 中的电流之和。即
中的电流之和。即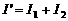 。由于
。由于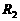 并联,所以
并联,所以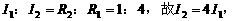
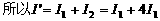
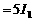 ,故
,故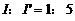 ,选C。
,选C。 均闭合时,
均闭合时, 消耗的功率之比为5:1,求
消耗的功率之比为5:1,求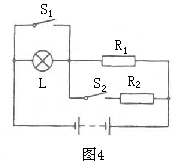
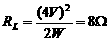

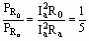
 (1)
(1)
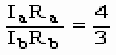
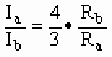 (2)
(2)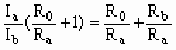
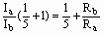 (3)
(3)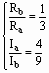
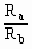 =
=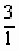 =3
=3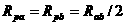 ,两电阻并联,
,两电阻并联,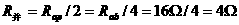 ,因U=6伏,故
,因U=6伏,故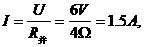
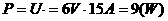
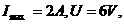 故
故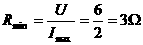
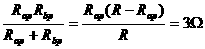
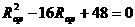
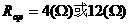 .
. )到12
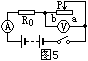
)到12 如图17-18所示电路中,滑动变阻器的滑片P把变阻器分为Rap和Rpb两部分,已知变阻器的最大阻值为16欧,电源电压为6伏不变,电流表的最大量程为2安,求:
如图17-18所示电路中,滑动变阻器的滑片P把变阻器分为Rap和Rpb两部分,已知变阻器的最大阻值为16欧,电源电压为6伏不变,电流表的最大量程为2安,求: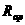 和
和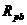 两部分,已知变阻器的最大值为
两部分,已知变阻器的最大值为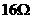 ,电源电压为6V不变,电流表的最大量程为2A。求:
,电源电压为6V不变,电流表的最大量程为2A。求: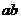 间的阻值范围。
间的阻值范围。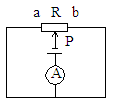
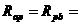
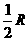 ;要求出P在中点时电流表示数,或用
;要求出P在中点时电流表示数,或用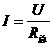 ,或根据并联电路干路电流等于各支路电流之和
,或根据并联电路干路电流等于各支路电流之和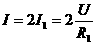 都可求出,变阻器的总功率可根据
都可求出,变阻器的总功率可根据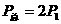 求出。
求出。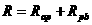 和
和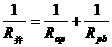 求出P片的滑动范围。
求出P片的滑动范围。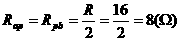 ,电流表示数
,电流表示数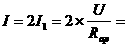
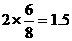 (A)
(A)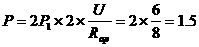 (A)
(A)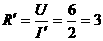 (
(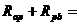 R,
R,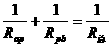 ,所以
,所以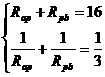
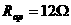 或
或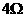 ,
,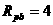
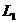 、
、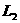 均可发光,当变阻器的滑片P向左移动时( )
均可发光,当变阻器的滑片P向左移动时( ) 
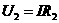 最小,L1两端电压最大,所以此时L1最亮,L2最暗。在P向左端移动时,变阻器连入电路的电阻逐渐变小,P达到最左端时,变阻器连入电路的电阻为零,L1被短路,L1不发光,电源电压全部加在灯L2两端,L2两端电压最大,通过L2的电流也最大,L2最亮,所以P向左移动L1变暗,L2变亮,C项正确。
最小,L1两端电压最大,所以此时L1最亮,L2最暗。在P向左端移动时,变阻器连入电路的电阻逐渐变小,P达到最左端时,变阻器连入电路的电阻为零,L1被短路,L1不发光,电源电压全部加在灯L2两端,L2两端电压最大,通过L2的电流也最大,L2最亮,所以P向左移动L1变暗,L2变亮,C项正确。 为定值电阻,变阻器的最大阻值是
为定值电阻,变阻器的最大阻值是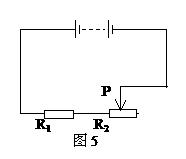
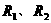 并联时的总电阻是
并联时的总电阻是 ,串联时的总电阻( )
,串联时的总电阻( )

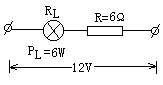 解:如图
解:如图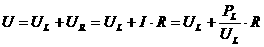
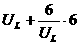
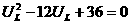
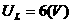
 .
.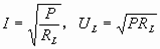
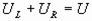
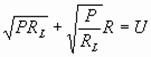
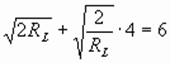
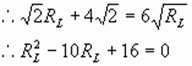
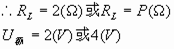
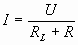
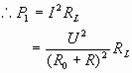
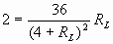
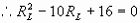
 的值
的值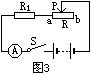 A、逐渐变大 B、逐渐变小
A、逐渐变大 B、逐渐变小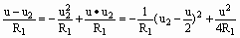 。
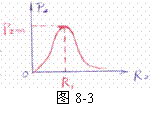
上式可视为一个二次函数,当u2=
。
上式可视为一个二次函数,当u2=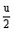 时,p2有最大值
时,p2有最大值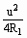 ,因R1、R2串联,所以有
,因R1、R2串联,所以有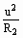 =
=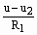 ,可得此时R2=R1。
,可得此时R2=R1。 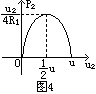 p2=u2·I=u2·
p2=u2·I=u2·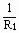 (u2-
(u2-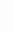 )2+
)2+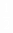 u(即R2=R1)时,p2最大为
u(即R2=R1)时,p2最大为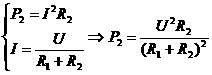 --①
--①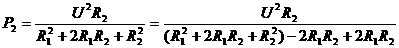 (给分母配方)
(给分母配方)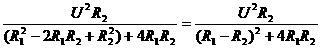
 将上式中分子分母同时除以
将上式中分子分母同时除以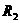 ,则有
,则有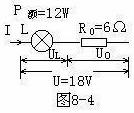
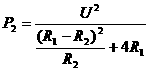 --②在上述电路中,R1、U都是定值.
--②在上述电路中,R1、U都是定值. 公式中R2是自变量,P2是因变量,即R2的函数,因此不难看出:当R2=R1时,R2消耗的功率最大,且最大功率
公式中R2是自变量,P2是因变量,即R2的函数,因此不难看出:当R2=R1时,R2消耗的功率最大,且最大功率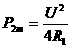 .
.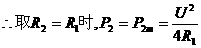 .
.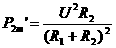 ,公式中的R2为滑动变阻器可连入的最大电阻.
,公式中的R2为滑动变阻器可连入的最大电阻.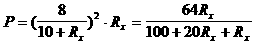 ,根据数学上方程
,根据数学上方程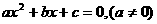 ,有实数根时,△=b2-4ac≥0求解。将上式整理为关于Rx的一元二次方程
,有实数根时,△=b2-4ac≥0求解。将上式整理为关于Rx的一元二次方程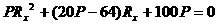 ,因为Rx存在且有正根,所以△=(20P-64)2-4×P×100P≥0,解不等式得P≤1.6瓦,所以R2消耗的最大电功率为1.6瓦,将P=1.6瓦代入原方程可以求得Rx=10Ω。
,因为Rx存在且有正根,所以△=(20P-64)2-4×P×100P≥0,解不等式得P≤1.6瓦,所以R2消耗的最大电功率为1.6瓦,将P=1.6瓦代入原方程可以求得Rx=10Ω。 的粗细均匀的电阻丝,绕成一个圆环,用导线在A点固定相接,滑片B与电阻丝接触良好,把它接在电压为12伏的电源上,求滑片至何处时电流表的示数最小,并求这个最小值。
的粗细均匀的电阻丝,绕成一个圆环,用导线在A点固定相接,滑片B与电阻丝接触良好,把它接在电压为12伏的电源上,求滑片至何处时电流表的示数最小,并求这个最小值。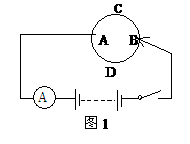
 ,则ADB段电阻为
,则ADB段电阻为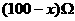 ,因为ACB段与ADB段并联,则
,因为ACB段与ADB段并联,则 ,
, 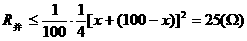 ,
, ,即
,即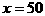 时成立,因此
时成立,因此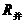 的最大值为
的最大值为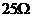 ,于是
,于是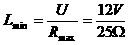
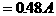
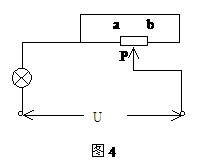
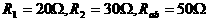 。闭合开关S,滑片P从b端向a端移动的过程中,电路中电流表的示数( )
。闭合开关S,滑片P从b端向a端移动的过程中,电路中电流表的示数( )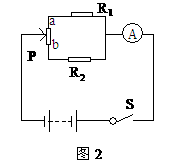
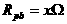 ,则
,则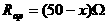 ,电路中的总电阻是由
,电路中的总电阻是由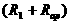 与
与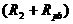 并联而得的总电阻。于是
并联而得的总电阻。于是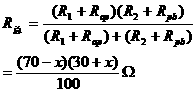
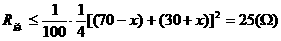
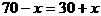 ,即
,即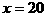 时成立,此时电路中的总电阻最大。可知,滑片P从b端向a端移动的过程中,电路中的总电阻先增大后减小,所以电路中的总电流先减少后增大,即电流表的示数先减小后增大,选D。
时成立,此时电路中的总电阻最大。可知,滑片P从b端向a端移动的过程中,电路中的总电阻先增大后减小,所以电路中的总电流先减少后增大,即电流表的示数先减小后增大,选D。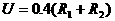 ,
,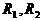 并联时,
并联时,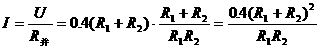
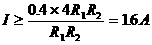
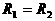 时,
时,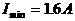
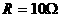 ,滑动变阻器的总阻值
,滑动变阻器的总阻值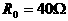 ,a与b为变阻器的上下端点,电源电压U=40V,求滑动变阻器滑到何处时,电流表读数最小?
,a与b为变阻器的上下端点,电源电压U=40V,求滑动变阻器滑到何处时,电流表读数最小?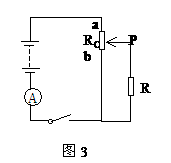
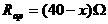
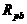 并联的电阻为
并联的电阻为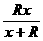 ,于是
,于是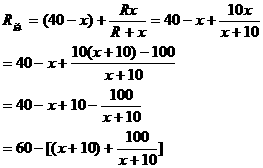
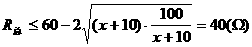
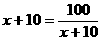 ,即
,即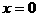 时
时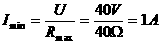
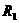 和
和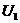 的电源上,消耗的总功率为
的电源上,消耗的总功率为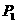 ,将
,将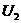 的电源上,消耗的总功率为
的电源上,消耗的总功率为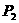 ,若
,若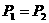 ,下面说法正确的是( )
,下面说法正确的是( )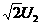
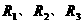 并联,总电流
并联,总电流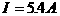 ,又
,又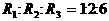 ,求通过
,求通过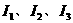
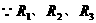 并联
并联