2、速度--时间图象的迁移与妙用
 [例4] 一个固定在水平面上的光滑物块,其左侧面是斜面AB,右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑,比较它们到达水平面所用的时间
[例4] 一个固定在水平面上的光滑物块,其左侧面是斜面AB,右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑,比较它们到达水平面所用的时间
A.p小球先到 B.q小球先到 C.两小球同时到 D.无法确定
解:可以利用v-t图象(这里的v是速率,曲线下的面积表示路程s)定性地进行比较。在同一个v-t图象中做出p、q的速率图线,显然开始时q的加速度较大,斜率较大;由于机械能守恒,末速率相同,即曲线末端在同一水平图线上。为使路程相同(曲线和横轴所围的面积相同),显然q用的时间较少。
 [例5] 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a/ 同时从管口由静止滑下,问谁先从下端的出口掉出?(假设通过拐角处时无机械能损失)
[例5] 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a/ 同时从管口由静止滑下,问谁先从下端的出口掉出?(假设通过拐角处时无机械能损失)
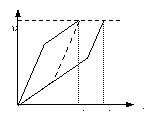 解:首先由机械能守恒可以确定拐角处v1> v2,而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律,小球的加速度大小a=gsinα,小球a第一阶段的加速度跟小球a/第二阶段的加速度大小相同(设为a1);小球a第二阶段的加速度跟小球a/第一阶段的加速度大小相同(设为a2),根据图中管的倾斜程度,显然有a1> a2。根据这些物理量大小的分析,在同一个v-t图象中两球速度曲线下所围的面积应该相同,且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等,如果同时到达(经历时间为t1)则必然有s1>s2,显然不合理。考虑到两球末速度大小相等(图中vm),球a/ 的速度图象只能如实线所示。因此有t1< t2,即a球先到。
解:首先由机械能守恒可以确定拐角处v1> v2,而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律,小球的加速度大小a=gsinα,小球a第一阶段的加速度跟小球a/第二阶段的加速度大小相同(设为a1);小球a第二阶段的加速度跟小球a/第一阶段的加速度大小相同(设为a2),根据图中管的倾斜程度,显然有a1> a2。根据这些物理量大小的分析,在同一个v-t图象中两球速度曲线下所围的面积应该相同,且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等,如果同时到达(经历时间为t1)则必然有s1>s2,显然不合理。考虑到两球末速度大小相等(图中vm),球a/ 的速度图象只能如实线所示。因此有t1< t2,即a球先到。
[例6]一只老鼠从洞口爬出后沿一直线运动,其速度大小与其离开洞口的距离成反比。当其到达距洞口为d1的A点时速度为v1.若B点离洞口的距离为d2(d2>d1),求老鼠由A运动至B所需的时间。
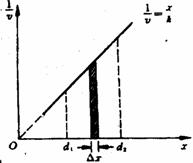 [解析]图中的曲线与横轴所围面积的数值正是老鼠经过一定的位移所需的时间。如图所示,取一窄条,其宽度Δx很小(Δx→0),此段位移所需时间Δt也很小(Δv→0),可以认为在如此短时间内,老鼠的速度改变很小(Δv→0),如图中窄条的面积为A=Δx
[解析]图中的曲线与横轴所围面积的数值正是老鼠经过一定的位移所需的时间。如图所示,取一窄条,其宽度Δx很小(Δx→0),此段位移所需时间Δt也很小(Δv→0),可以认为在如此短时间内,老鼠的速度改变很小(Δv→0),如图中窄条的面积为A=Δx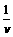 =
=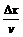 ,这正表示老鼠经位移Δx所需的时间。故图中,图线
,这正表示老鼠经位移Δx所需的时间。故图中,图线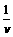 =
= ,x1=dl,x2=d2及x轴所围的梯形面积正是老鼠由dl爬至d2所需的时间。K=v1d1=v2d2;T=
,x1=dl,x2=d2及x轴所围的梯形面积正是老鼠由dl爬至d2所需的时间。K=v1d1=v2d2;T=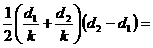
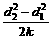
 。
。
说明:利用图象的物理意义来解决实际问题往往起到意想不到的效果.在中学阶段某些问题根本无法借助初等数学的方法来解决,但如果注意到一些图线的斜率和面积所包含的物理意义,则可利用比较直观的方法解决问题。
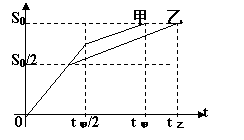
[例7]甲、乙两车同时同向沿直线驶向某地,甲在前一半时间以v1匀速运动,后一半时间以v2匀速运动.乙在前一半路程以v1匀速运动,后一半路程以v2匀速运动,先到目的地的是____.
|
[例8]质点P以O点为平衡位置竖直向上作简谐运动,同时质点Q也从O点被竖直上抛,它们恰好同时到达最高点,且高度相同,在此过程中,两质点的瞬时速度vP与vQ的关系应该是 [ D ]
 A.vP>vQ. B.先vP>vQ,后vP<vQ,最后vP=vQ=0.
A.vP>vQ. B.先vP>vQ,后vP<vQ,最后vP=vQ=0.
C.vP<vQ. D.先vP<vQ,后vP>vQ,最后vP=vQ=0.
解析:这也是用解析方法很难下手的题目,但若能利用题设条件,画好、分析好两个质点的v-t图线,就能很快找到答案.
先在图中画出Q作匀减速运动的v-t图象.由于P作简谐运动,当它由平衡位置向极端位置运动过程中,受到的回复力从零开始不断变大,它的加速度也从零开始不断变大,速度不断变小,P作加速度不断增大的减速运动,其v-t图线是一条曲线.根据v-t图线上任一点的切线的斜率数值上等于质点在该时刻的加速度,由于P的加速度由零开始不断变大,画出曲线切线斜率的绝对值也应由零开始不断增大,即曲线的切线应从呈水平状态开始不断变陡,那么只有向右边凸出的下降的曲线才能满足这样的条件.又因P与Q的运动时间相等,所以曲线的终点也应在t,P与Q的路程相等,所以曲线包围的面积应等于三角形vQ0Ot的面积,根据这些要求,曲线的起点,即质点P的初速度vP0必定小于Q的初速vQ0,且两条v-t图线必定会相交,如图7中的实线所示.图7的两条虚线表示的质点P的v-t图线都不满足题设条件(P与Q的路程相等),所以(D)选项正确.
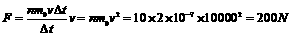
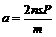
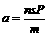
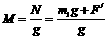 =m1+m2+Δm
=m1+m2+Δm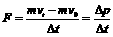
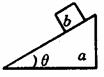 [例1]如图所示,在粗糙水平面上放一三角本块a,若物体b在a的斜面上静止,加速,匀速或减速下滑时.在四种情况下a对平面的压力比a、b两重力之和大还是小?
[例1]如图所示,在粗糙水平面上放一三角本块a,若物体b在a的斜面上静止,加速,匀速或减速下滑时.在四种情况下a对平面的压力比a、b两重力之和大还是小? Ny=Nb-acosθ=Gbcos2θ
Ny=Nb-acosθ=Gbcos2θ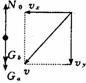 解法二:将a、b视为一整体如图所示,将N分解
解法二:将a、b视为一整体如图所示,将N分解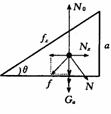 (4)当b沿斜面向上运动.
(4)当b沿斜面向上运动.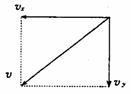 解法二:将ab视为一个系统,将b的速度分解如图所示,
解法二:将ab视为一个系统,将b的速度分解如图所示,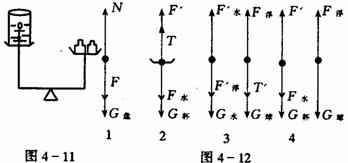 解法一:按照常规则应进行如下分析
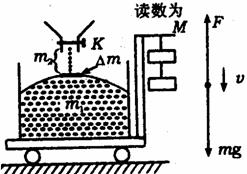
解法一:按照常规则应进行如下分析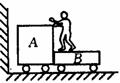 [例3]如图所示,在光滑水平面上,有A、B两辆小车.水平面左侧有一竖直墙.在小车B上坐着一个小孩.小孩与车B的总质量是车A的10倍,两车从静止开始,小孩把车A以对地速度v推出,车A与墙碰撞后仍以原速率返回,小孩接到车A后,又把它以对地速度v推出,车A返回后,小孩再把它推出,每次推出,小车A对地速度都是v,方向向左,则小孩共把车A推出多少次后,车A返回小孩不能再接到?
[例3]如图所示,在光滑水平面上,有A、B两辆小车.水平面左侧有一竖直墙.在小车B上坐着一个小孩.小孩与车B的总质量是车A的10倍,两车从静止开始,小孩把车A以对地速度v推出,车A与墙碰撞后仍以原速率返回,小孩接到车A后,又把它以对地速度v推出,车A返回后,小孩再把它推出,每次推出,小车A对地速度都是v,方向向左,则小孩共把车A推出多少次后,车A返回小孩不能再接到? v≥v
则 n≥5.5, n取整数, n=6次后,车A 返回时,小孩接不到车A
v≥v
则 n≥5.5, n取整数, n=6次后,车A 返回时,小孩接不到车A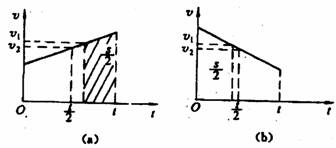 注意:平均速率不是平均速度的大小.对于图象问题,要求把运动物体的实际运动规律与图象表示的物理含义结合起来考虑.
注意:平均速率不是平均速度的大小.对于图象问题,要求把运动物体的实际运动规律与图象表示的物理含义结合起来考虑.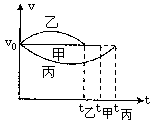 [解析]由题意,作出物体的v一t关系图,½S点处的虚线把梯形面积一分为二,如图所示,由图可知,无论物体作匀加速直线运动还是作匀减速直线运动。在路程中间位置的速度v1始终大于中间时刻的速度v2,当物体作匀速直线运动时,在任何位置和任何时刻的速度都相等。
[解析]由题意,作出物体的v一t关系图,½S点处的虚线把梯形面积一分为二,如图所示,由图可知,无论物体作匀加速直线运动还是作匀减速直线运动。在路程中间位置的速度v1始终大于中间时刻的速度v2,当物体作匀速直线运动时,在任何位置和任何时刻的速度都相等。 说明:图象法是根据物体的运动规律及题中条件,将复杂的运动过程转化成简单、直观过程的一种思维方法。
说明:图象法是根据物体的运动规律及题中条件,将复杂的运动过程转化成简单、直观过程的一种思维方法。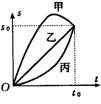 规律方法
规律方法 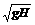 两物体相遇时,B正在上升途中 B、v0=
两物体相遇时,B正在上升途中 B、v0=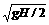 <v0<
<v0<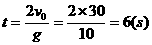
 ,将t1=3.5s,t2=4.0s,t3=4.5s,t4=5.0s和 t5=5.5s分别代入上式,得h1=43.75m,h2=40m,h3=33.75m,h4=25m,h5=13.75m。
,将t1=3.5s,t2=4.0s,t3=4.5s,t4=5.0s和 t5=5.5s分别代入上式,得h1=43.75m,h2=40m,h3=33.75m,h4=25m,h5=13.75m。
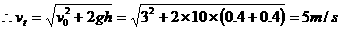
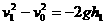
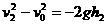
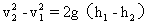 ,
,
 ;
;  ;
;
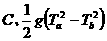 ;
; 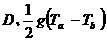
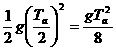 ,b点到最高点的距离hb=
,b点到最高点的距离hb=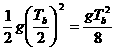 ,
,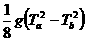 ,即选A
,即选A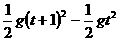 ,即93.1=
,即93.1=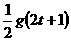 ,解得 t=9(s)
,解得 t=9(s)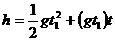 ,即
,即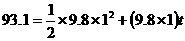 解得 t=9(s)
解得 t=9(s)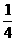 h0。从开始计时到第n个水滴落到盘子中,共有(n+1)个水滴离开水龙头,相邻两滴水滴落下的时间间隔为t1=
h0。从开始计时到第n个水滴落到盘子中,共有(n+1)个水滴离开水龙头,相邻两滴水滴落下的时间间隔为t1=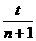 。
。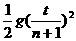 得:g=
得:g=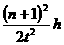
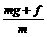 ,a下=
,a下= ,所以a上>a下. t上=
,所以a上>a下. t上=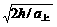 ,t下=
,t下=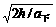 。所以t上<t下,v0=
。所以t上<t下,v0=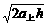 ,vt=
,vt=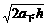 ,所以v0>vt 答案:C
,所以v0>vt 答案:C