29.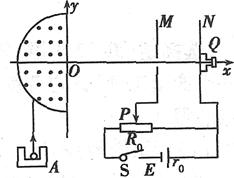 湖南师大附中2010届高三第五次月考试卷如图所示,某放射源A中均匀地向外辐射出平行于y轴的速度一定的α粒子,粒子质量为m,电荷量为q.为测定其从放射源飞出的速度大小,现让α粒子先经过一个磁感应强度为B、区域为半圆形的匀强磁场,经该磁场偏转后,它恰好能够沿x轴进入右侧的平行板电容器,并打到置于板N的荧光屏上出现亮点.当触头P从右端向左移动到滑动变阻器的中央位置时,通过显微镜头Q看到屏上的亮点恰好能消失.已知电源电动势为E,内阻为r0,滑动变阻器的总电阻R0=2 r0,求:
湖南师大附中2010届高三第五次月考试卷如图所示,某放射源A中均匀地向外辐射出平行于y轴的速度一定的α粒子,粒子质量为m,电荷量为q.为测定其从放射源飞出的速度大小,现让α粒子先经过一个磁感应强度为B、区域为半圆形的匀强磁场,经该磁场偏转后,它恰好能够沿x轴进入右侧的平行板电容器,并打到置于板N的荧光屏上出现亮点.当触头P从右端向左移动到滑动变阻器的中央位置时,通过显微镜头Q看到屏上的亮点恰好能消失.已知电源电动势为E,内阻为r0,滑动变阻器的总电阻R0=2 r0,求:
(1) α粒子从放射源飞出速度的大小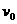 ;
;
(2)满足题意的α粒子在磁场中运动的总时间t;
(3)该半圆形磁场区域的半径R.

|
|||||||
|
|||||||
|
|||||||
 |
 .1,取g=10m/s2。
.1,取g=10m/s2。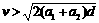 ,则两车一定不会相撞
,则两车一定不会相撞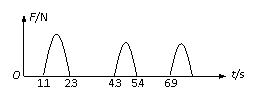 D.若
D.若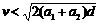 ,则两车一定不会相撞
,则两车一定不会相撞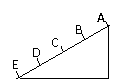 物体到达各点的速率之比 vB:vC:vD:vE=1:
物体到达各点的速率之比 vB:vC:vD:vE=1: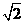 :
: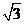 :2
:2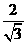 tD
tD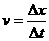 ,当
,当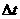 非常非常小时,
非常非常小时,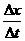 就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法
就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法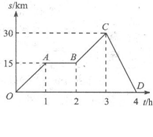 福建省泉州市四校2010届高三上学期期末联考如图是一辆汽车做直线运动的s-t图像,对线段OA、AB、BC、CD所表示的运动,下列说法正确的是
( C )
福建省泉州市四校2010届高三上学期期末联考如图是一辆汽车做直线运动的s-t图像,对线段OA、AB、BC、CD所表示的运动,下列说法正确的是
( C )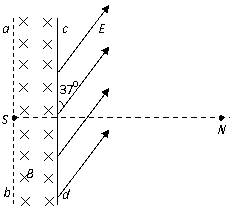 湖南省雅礼中学2010届高三上学期第五次月考如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q = 3.2×10-19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求:
湖南省雅礼中学2010届高三上学期第五次月考如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q = 3.2×10-19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求: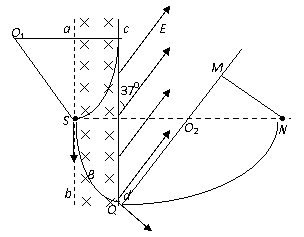 解:(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即
解:(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即 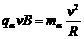 (1分)
(1分)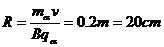 (2分)
(2分) (1分)
(1分) 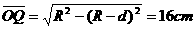 (1分)
(1分) (1分)
(1分)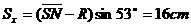 (1分)
(1分)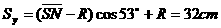 (1分)
(1分)
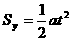
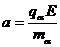 得:
得: 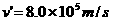 (2分)
(2分)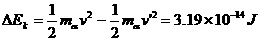 (2分)
(2分)
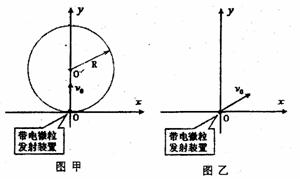 浙江省金华一中2010届高三12月联考如图甲所示,x轴正方向水平向右,y轴正方向竖直向上。在xoy平面内有与y轴平行的匀强电场,在半径为R的圆形区域内加有与xoy平面垂直的匀强磁场。在坐标原点O处放置一带电微粒发射装置,它可以连续不断地发射具有相同质量m、电荷量q(
浙江省金华一中2010届高三12月联考如图甲所示,x轴正方向水平向右,y轴正方向竖直向上。在xoy平面内有与y轴平行的匀强电场,在半径为R的圆形区域内加有与xoy平面垂直的匀强磁场。在坐标原点O处放置一带电微粒发射装置,它可以连续不断地发射具有相同质量m、电荷量q(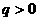 )和初速为
)和初速为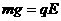 1分
1分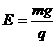 1分
1分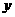 轴正方向
轴正方向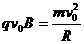 1分
1分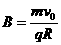 1分
1分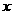 轴承夹角
轴承夹角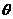 ,
,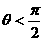 ,由于带电微粒最终将沿
,由于带电微粒最终将沿 平面向外,带电微粒在磁场内做半径为
平面向外,带电微粒在磁场内做半径为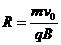 匀速圆周运动。
匀速圆周运动。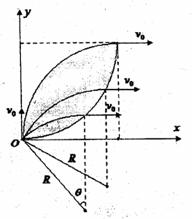 由图可知,它们必须从经O点作圆运动的各圆的最高点飞离磁场。
由图可知,它们必须从经O点作圆运动的各圆的最高点飞离磁场。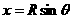 ,
,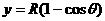 ,
,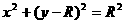 2分
2分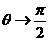 的角度射入磁场区域的微粒的运动轨迹
的角度射入磁场区域的微粒的运动轨迹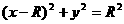
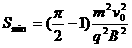 1分
1分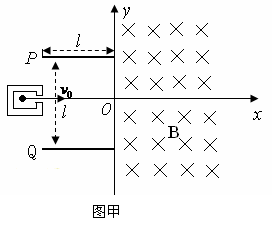 河南省武陟一中2010届高三第一次月考如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴向右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子。在0~3t0时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、l、l0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)(1)求电压U的大小。(2)求 t0时进入两板间的带电粒子在磁场中做圆周运动的半径。(3)何时进入两板间的带电粒子在磁场中的运动时间最短?求此最短时间。
河南省武陟一中2010届高三第一次月考如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴向右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子。在0~3t0时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、l、l0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)(1)求电压U的大小。(2)求 t0时进入两板间的带电粒子在磁场中做圆周运动的半径。(3)何时进入两板间的带电粒子在磁场中的运动时间最短?求此最短时间。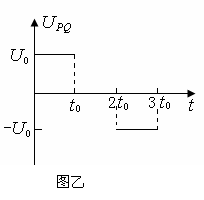
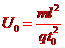 (2)
(2)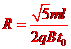 (3)
(3)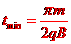
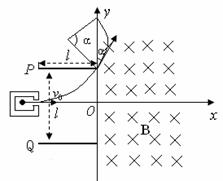 [解析](1)t=o时刻进入两极板的带电粒子在电场中做匀变速曲线运动,t0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为l/2,则有
[解析](1)t=o时刻进入两极板的带电粒子在电场中做匀变速曲线运动,t0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为l/2,则有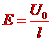 ①
①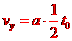 ⑥
⑥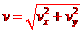 ⑦
⑦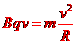 ⑧
⑧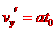 ⑩,
⑩, ,则
,则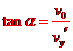 ,
,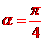 ,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为
,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为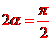 ,所求最短时间为
,所求最短时间为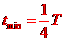 ,带电粒子在磁场中运动的周期为
,带电粒子在磁场中运动的周期为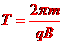 ,联立以上两式解得
,联立以上两式解得